Datenbanksysteme Klausurvorbereitung

Entwurfstheorie

Funktionale Abhängigkeiten

• Funktionale Abhängigkeiten (functional dependencies oder FD) sind statische Integritätsbedingungen. Diese sind semantische Bedingungen, um die Menge der Datenbankzustände einzuschränken.
• FDs sind Teil der Informationsanforderungen und werden in Absprache mit dem Anwender bei der Anforderungsanalyse gewonnen

Definition - funktionale Abhängigkeit:

Seien $A, B ⊆ RS$ Teilmengen eines Relationenschemas $RS$. $B$ ist von $A$ funktional abhängig oder $A$ bestimmt $B$ funktional, geschrieben $A → B$, genau dann wenn zu jeder Relation $r \in REL(RS)$ und jedem Wert in $A$ genau ein Wert in $B$ gehört:

• Für alle $t_1, t_2 \in r: t_1[A] = t_2[A] ⇒ t_1[B] = t_2[B]$

Beispiel

Lieferant($\underline{LName}, LAdr, \underline{Ware}, Preis$)

• Funktionale Abhängigkeiten:

  • {LName} → {LAdr}

    • ein Lieferantenname bestimmt eindeutig seine Adresse

  • {LName, Ware} → {Preis}

    • {LName, Ware} bestimmt eindeutig den Preis

  • {LName} → {LName} (trivial)

  • {LName, Ware} → {Ware} (trivial)

  • {LName, Ware} → {LAdr} (partiell)

Überprüfung von FDs

Funktionale Abhängigkeiten sind wichtige Regeln, um die Datenqualität sicherzustellen. Sollte in einer Relation $r$ die FD $A → B$ erfüllt sein, so darf folgende SQL-Anfrage kein Ergebnis liefern:

select A, count(distinct B)
from r
group by A
having (count(distinct B) > 1)

Diese Überprüfung garantiert aber nicht, dass auch zukünftig die FD erfüllt ist.

Funktionale Abhängigkeiten sind wichtige Regeln, um die Datenqualität sicherzustellen.

• Beim Einfügen eines neuen Tupels (..., a, ..., b, ...) in die Relation $r$ muss vorher überprüft werden, ob die folgende Anfrage leer ist:

xxxxxxxxxx
select *
from r
where A = a and B <> b

Ziel von FDs

• Hohe Datenqualität

  • Erfassung aller funktionaler Abhängigkeiten in einer Anwendung → Menge $F$ von FDs

• Geringe Kosten, um die Datenqualität zu prüfen

  • Anlegen eines Index für jede FD

  • Zwar kann jede FD in logarithmischer Zeit geprüft werden, aber die Anzahl der FDs kann sehr hoch sein

  • Minimierung der Anzahl der FDs

    • Gibt es eine zu $F$ äquivalente Menge $F_c$, die

      • mit weniger FDs als $F$ auskommt
      • und jede FD aus F auch aus $F_c$ abgeleitet werden kann?

Vorgehensweise - Minimierung der Anzahl der FDs

Ziel: Zu einer gegebenen Menge $F$ an FDs soll eine möglichst kleine äquivalente Menge $F_c$ von FDs berechnet werden.

• Naiver Ansatz

  • Ableitung aller FDs für eine vorgegebene Menge $F$ → Hülle $F^+$
  • Teste, ob eine FD in $F^+$ liegt

• Effizienterer Ansatz

  • Direkte Überprüfung, ob eine FD $A → B$ aus einer vorgegebenen Menge $F$ ableitbar ist.

  • Erstellung einer minimalen Repräsentantenmenge $F_c$, so dass alle FDs in $F$ aus $F_c$ ableitbar sind

    • Beim Einfügen eines neuen Tupels genügt es die Regeln in $F_c$ zu überprüfen

• Vorgehensweise

  1. Berechne aus $F$ die Menge $F^+$ aller aus $F$ ableitbaren FDs
  2. Verkleinere F so, dass aus der reduzierten Menge immer noch $F^+$ abgeleitet werden kann

Definition - Besondere FDs

• Eine FD $A → B$ ist trivial, wenn gilt $B ⊆ A$

• Eine FD $A → B$ heißt voll, wenn es keine echte Teilmenge $C ⊆ A$ gibt, so dass $C → B$ gilt.

  • Gibt es eine solche Teilmenge $C$, dann heißt $A → B$ partielle Abhängigkeit

• Seien $A, B ⊆ RS$ und $A → B$ (aber nicht $B → A$). Sei $X \in RS - (A \cup B)$ und gelte $B → \{X\}$. Dann ist $\{X\}$ transitiv abhängig von $A: A →\{X\}$

Hülle einer Menge von FDs

• Zu einer gegebenen Menge $F$ von FDs soll $F^+$ die Menge aller gültigen FDs berechnet werden.

  • $F^+$ wird als die Hülle von $F$ bezeichnet.

• Zur Berechnung von $F^+$ werden folgende Regeln genutzt (Armstrong Axiome):

  • Reflexivität: Sei $B⊆ A$. Dann gilt stehts $A \rightarrow B$
  • Verstärkung: Falls $A \rightarrow B$ gilt, dann gilt auch $A \cup C \rightarrow B \cup C$
  • Transitivität: Falls $A \rightarrow B$ und $B \rightarrow C$, dann gilt auch $A \rightarrow C$

Alle gültigen FDs in $F^+$ können mit Hilfe dieser Regeln auch hergeleitet werden.

Ableitungsregeln

Trotz der Eigenschaften der Armstrong-Axiome ist es komfortabler noch folgende Regeln zu benutzen:

• Vereinigungsregel: Falls $A \rightarrow B$ und $A \rightarrow C$ gilt, dann gilt auch $A \rightarrow B \cup C$
• Dekompositionsregel: Falls $A \rightarrow B \cup C$ gilt, dann gilt auch $A \rightarrow B$ und $A \rightarrow C$
• Pseudotransivität: Falls $A \rightarrow B$ und $B \cup C \rightarrow D$ gilt, dann auch gilt auch $A \cup C \rightarrow D$

Berechnung Hülle per Algorithmus

Algorithmus zur Berechnung der Hülle mit gegebenen F (Menge der FDs einer Anwendung) und A (alle Attribute die von A funktional bestimmt werden)

xxxxxxxxxx
Hülle(F,A):
Erg = A // A → A trivial
While(Erg ändert sich):
  Foreach(B → C in F):
    if(B ⊆ Erg):
      Erg = Erg + C
return Erg

Beispiel: Hüllenberechnung

$F = \{\{A\} \rightarrow \{B\}, \{B\} \rightarrow \{D, E\}, \{C,E\} \rightarrow \{B,F\}, \{F\} \rightarrow \{G\}\}$

Gesucht ist Hülle$(F,\{A\}) = A^+$

1. $A_0^+$ = $\{A\}$
2. $A_1^+$ = $\{A, B\}$
3. $A_2^+$ = $\{A, B, D, E\}$
4. $A^+_3$ = $\{A, B, D, E\}$ und der Algorithmus terminiert
5. $A^+$ = $\{A, B, D, E\}$

Erklärung zu den einzelnen Schritten:

1. Trivialer Fall, Füge $A$ hinzu (noch vor der Schleife im Algorithmus)
2. Wir gehen in die Schleife und schauen, ob die linken Seiten unserer FDs jeweils schon vollständig im Ergebnis ($A_0^+$) enthalten sind. Dies ist offensichtlich bei $\{A\} \rightarrow \{B\}$ der Fall, also können wir $B$ unserem Ergebnis hinzufügen.
3. Da die FD $\{B\} \rightarrow \{D, E\}$ existiert und $B$ eine Teilmenge des Ergebnis $(A_1^+)$ ist, kann $D$ und $E$ dem Ergebnis hinzugefügt werden.

Kanonische Überdeckung

Ziel: Minimierung der FDs einer Anwendung (Menge $F$)

• Finden einer äquivalenten Menge $F_c$, die mit weniger FDs auskommt
• Dazu bilden der Hülle $F^+$
• Anschließendes Verkleinern der Menge ohne Informationsverlust
• Finden der kanonischen Überdeckung $F_c$, so dass $F_c$ minimale Repräsentantenmenge mit $F_c^+$ = $F^+$

Algorithmus

Gegeben: Menge $F$ mit funktionalen Abhängigkeiten

1. Führe für jede FD $A \rightarrow B$ aus F die Linksreduktion durch:

   Überprüfe für alle $X \in A$, ob $X$ überflüssig ist, d.h. ob $B ⊆$ Hülle$(F, A-X)$

   Ist dies der Fall, ersetze in $F$ $A \rightarrow B$ durch $(A-X) \rightarrow B$

2. Führe für jede verbliebende FD $A \rightarrow B$ die Rechtsreduktion durch:

   Überprüfe für alle $Y \in B$, ob $Y$ überflüssig ist, d.h. ob $Y \in$ Hülle$(F - \{A \rightarrow B\} \cup \{A \rightarrow (B-Y)\}, A)$

   Ist dies der Fall, wird $A \rightarrow B$ durch $A \rightarrow (B-Y)$ ersetzt

3. Entferne die FDs der Form $A \rightarrow \empty$ (die im 2-ten Schritt entstanden sind)

4. Ersetze alle FDs der Form $A \rightarrow B_1, ..., A \rightarrow B_k$ durch $A \rightarrow B_1 \cup$ ... $\cup B_k$

Beispiel: Berechnung kanonische Überdeckung

$F = \{\{A, B\} \rightarrow \{C\}, \{B\} \rightarrow \{A\}, \{C\} \rightarrow \{D\}, \{D\} \rightarrow \{A\}, \{D\} \rightarrow \{B\}\}$

Schritt 1: Linksreduktion

Info: Einelementige linke Seiten werden übersprungen.

$\{A, B\} \rightarrow \{C\}$, A ist überflüssig, da $A$ in der Hülle von $B$ enthalten ist: $A \in$ Hülle$(F, B) = \{A, B, C, D\}$. Ersetze also $\{A, B\} \rightarrow \{C\}$ mit $\{B\} \rightarrow \{C\}$.

Wir erhalten also: $F_1 = \{\{B\} \rightarrow \{C\}, \{B\} \rightarrow \{A\}, \{C\} \rightarrow \{D\}, \{D\} \rightarrow \{A\}, \{D\} \rightarrow \{B\}\}$

Schritt 2: Rechtsreduktion

Fragestellung bei der ersten FD $\{B\} \rightarrow \{C\}$: Kommen wir, wenn wir $C$ weglassen trotzdem irgendwie von $B$ nach $C$? Antwort: Nein! Wir kommen von $B$ nur nach $A$, aber von $A$ nicht mehr weiter. $C$ muss also weiterhin enthalten bleiben.

Führt man diesen Schritt für alle FDs aus erhält man:

$F_2 = \{\{B\} \rightarrow \{C\}, \{B\} \rightarrow \empty, \{C\} \rightarrow \{D\}, \{D\} \rightarrow \{A\}, \{D\} \rightarrow \{B\}\}$

Schritt 3: Entferne FDs der Form $A \rightarrow \empty$

$F_3 = \{\{B\} \rightarrow \{C\}, \{C\} \rightarrow \{D\}, \{D\} \rightarrow \{A\}, \{D\} \rightarrow \{B\}\}$

Schritt 4: Fasse alle FDs mit gleicher linker Seite zu einer zusammen

$F_4 = \{\{B\} \rightarrow \{C\}, \{C\} \rightarrow \{D\}, \{D\} \rightarrow \{A, B\}\} = F_c$

Verlustlosigkeit, Hüllentreue Zerlegung

Zerlegung von Relationen

• Zur Vermeidung von Anomalien zerlegen wir die Relation $R$ in $n$ Relationen $r_1, ..., r_n$
• Es darf kein Informationsverlust entstehen und die ursprüngliche Relation muss (durch z.B. natural join) reproduzierbar sein

Definition verlustlose Zerlegung:

• Sei $R$ zerlegt in $R_1$ und $R_2$, die Zerlegung ist verlustlos, falls:

  $(RS_1 \cap RS_2) \rightarrow RS_1 \in F_{RS}^+ \or (RS_1 \cap RS_2) \rightarrow RS_2 \in F_{RS}^+$

Zusätzlich wollen wir, dass die FDs lokal auf den zerlegten Relationen prüfbar sind, daraus ergibt sich folgende Definition.

Definition hüllentreue Zerlegung:

• Seien $F_1, ..., F_n$ lokale Mengen von FDs für die Relationen $r_1, ..., r_n$. Eine Zerlegung heißt hüllentreu, falls gilt:

  $F^+$ = $(F_1 \cup ... \cup F_n)^+$

Beispiel: Zerlegung

$F_{RS} = \{\{A\} \rightarrow \{B\}, \{B\} \rightarrow \{C\}, \{A\} \rightarrow \{D,E\}\}$

Sei $RS_1 = \{B, C\}$ und $RS_2 = \{A, B, D, E\}$ eine Zerlegung von RS. Zeigen oder widerlegen Sie, ob die folgende Zerlegung von $RS$ verlustlos und hüllentreu ist.

Verlustlosigkeit:

Aus der Definition folgt, dass entweder $(RS_1 \cap RS_2) \rightarrow RS_1 \in F_{RS}^+$ oder $(RS_1 \cap RS_2) \rightarrow RS_2 \in F_{RS}^+$ gelten muss.

Wir sehen, dass $RS_1 \cap RS_2 \rightarrow RS_2$ also $\{B\} \rightarrow \{B, C\} \in F_{RS}^+$ gilt. Somit ist die Zerlegung verlustlos.

Hüllentreue:

Hierfür schauen wir, ob alle FDs aus $F_{RS}$ in den beiden Schemata $RS_1$ und $RS_2$ "untergebracht" werden können. Beispielsweise könnte $\{A\} \rightarrow \{B\}$ in $RS_2$ untergebracht werden, da sowohl $A$, als auch $B$ in dieser Relation enthalten sind. Somit ergibt sich:

$F_{RS1} = \{\{B\} \rightarrow \{C\}\}$

$F_{RS2} = \{\{A\} \rightarrow \{B\}, \{A\} \rightarrow \{D, E\}\}$

Also $(F_{RS1} \cup F_{RS2})^+ = F_{RS}^+$ und somit ist die Zerlegung auch hüllentreu.

Normalformen

Normalformen sollen einen guten Datenbankentwurf garantieren.

Schlüsselkandidaten: Gibt es mehrere Schlüssel in einer Relation, nennt man diese auch Schlüsselkandidaten Prime Attribute: Attribute, die Teil eines Schlüsselkandidaten sind Nicht-Prime Attribute: Attribute, die nicht Teil eines Schlüsselkandidaten sind

1. Normalform

Alle Attribute können nur atomare, nicht weiter zerlegbare Werte annehmen.

2. Normalform

Jedes Nicht-Prime Attribut ist von jedem Schlüsselkandidaten voll funktional abhängig.

In diesem Beispiel ist TeilMenge voll funktional vom Schlüsselkandidaten (ProjektId, TeilId) abhängig. Projektleiter ist jedoch nur von ProjektId abhängig, daher wäre es nur partiell und nicht voll funktional vom Schlüsselkandidaten abhängig. Also muss die Relation in zwei Relationen aufgeteilt werden, um die 2. NF zu erhalten.

Info: 2. NF kann nur verletzt sein, wenn der Schlüssel zusammengesetzt ist.

3. Normalform

Es gibt kein Nicht-Prime Attribut, welches von einem Schlüsselkandidaten transitiv abhängig ist.

Projektleiter ist direkt abhängig von ProjektId, ProjektLeiterEmail jedoch nur von Projektleiter und somit transitiv vom abhängig vom Schlüsselkandidaten. Um die Relation in die 3. NF zu bringen muss auch hier wieder eine neue Relation erzeugt werden.

Synthesealgorithmus für die 3. NF (wenn es komplexer wird)

Ziel: Zerlegung einer Universalrelation in Relationen unter folgenden Bedingungen:

• Kein Informationsverlust
• Bewahrung der funktionalen Abhängigkeiten
• Die erzeugten Relationen erfüllen die 3. NF

Eingabe:

• Menge der Attribute $U$
• Menge der FDs $F$

Ausgabe:

• Relationenschemata in 3. NF

Ablauf:

1. Berechnung der kanonischen Überdeckung $F_c$ von $F$

2. Für jede $A \rightarrow B \in F_c$:

   • Erzeuge Relationenschema $RS_1 = A \cup B$
   • Ordne $RS_1$ alle FDs $F_1 = \{C \rightarrow D | C \cup D ⊆ RS_1\}$ zu

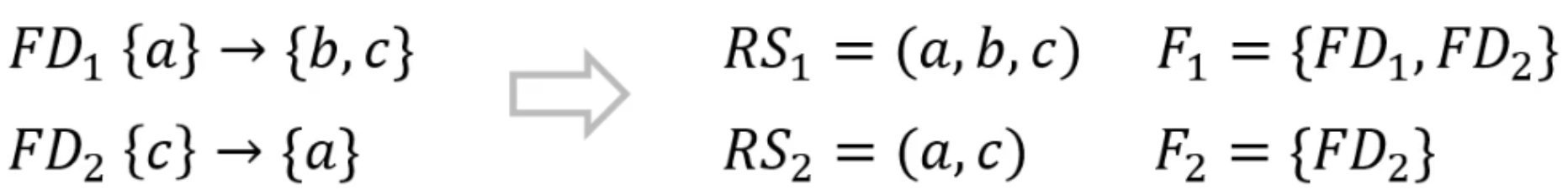
3. Falls kein erzeugtes Schema den Kandidatenschlüssel $K$ von $U$ enthält, erzeuge Relation mit Schema $RS_K = K$ und $F_K = \empty$.

   • Nur wenn der Kandidatenschlüssel nicht schon vollständig in einer der Relationen enthalten ist. Diese Relation hat dann genau die Attribute des Schlüsselkandidaten und keine funktionalen Abhängigkeiten

4. Eliminiere alle Schemata, die in einem anderen Schema enthalten sind.

   • Beispiel: $RS_2$ ist im obigen Beispiel bereits vollständig in $RS_1$ enthalten und kann somit eliminiert werden.

Synthesealgorithmus liefert ein Datenbankschema mit folgenden Eigenschaften:

1. Alle Relationen sind in der 3. NF
2. Hüllentreu
3. Kein Informationsverlust

Beispiel: Synthesealgorithmus bei gegebener kanonischer Überdeckung

$F_c = \{\{B\}\rightarrow \{C,E,F\}, \{A\} \rightarrow \{C,D,E\}, \{D,E\} \rightarrow \{A,F\}\}$

Schritt 2 (Relationenschemata erzeugen):

$R_1: (B, C, E, F)$ mit FDs $\{B\} \rightarrow \{C,E,F\}$ $R_2: (A,C,D,E)$ mit FDs $\{A\} \rightarrow \{C,D,E\}$ $R_3: (A,D,E,F)$ mit FDs $\{D,E\} \rightarrow \{A,F\}$

Schritt 3:

Da Schlüsselkandidat in diesem Beispiel unbekannt, muss man diesen erst herausfinden: Alle Attribute können über $A$ und $B$ erreicht werden, daher ist der Schlüssel $(A, B)$. Da $(A, B)$ in keiner der Relationen aus Schritt 2 vollständig enthalten ist, muss entsprechend eine 4. Relation erzeugt werden:

$R_4: (A, B)$

Schritt 4:

Keine Relation kann eliminiert werden, da keine Relation $R_i$ vollständig in einer anderen Relation $R_j$ enthalten ist.