2D-Transformationen

sämtliche Transformationen gehen vom Zentrum des Koordinatensystems aus, nicht vom Mittelpunkt des Objektes

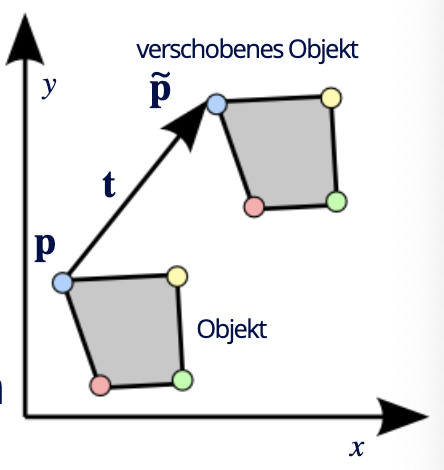
2D-Translation

• Veränderung der Position
• gegebener Stützpunkt $p$$p$ wird durch Verschiebung in x- und y-Richtung zu neuem Stützpunkt $\tilde{p}$$\tilde p$

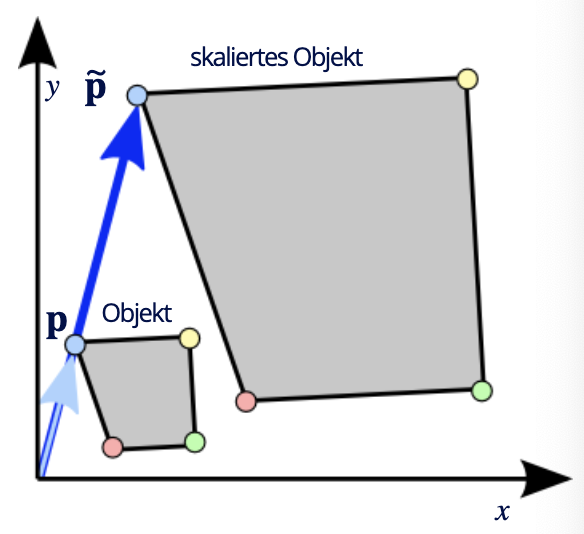
2D-Skalierung

• Veränderung der Größe

• Multiplikation mit Skalierungsfaktor(en) $s$$s$ ($s_x,s_y$$s_x, s_y$)

  

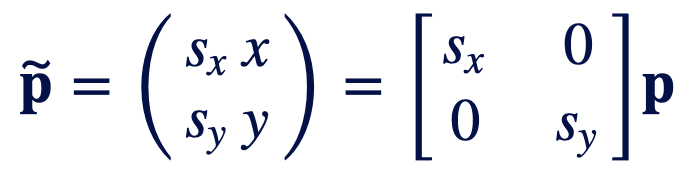
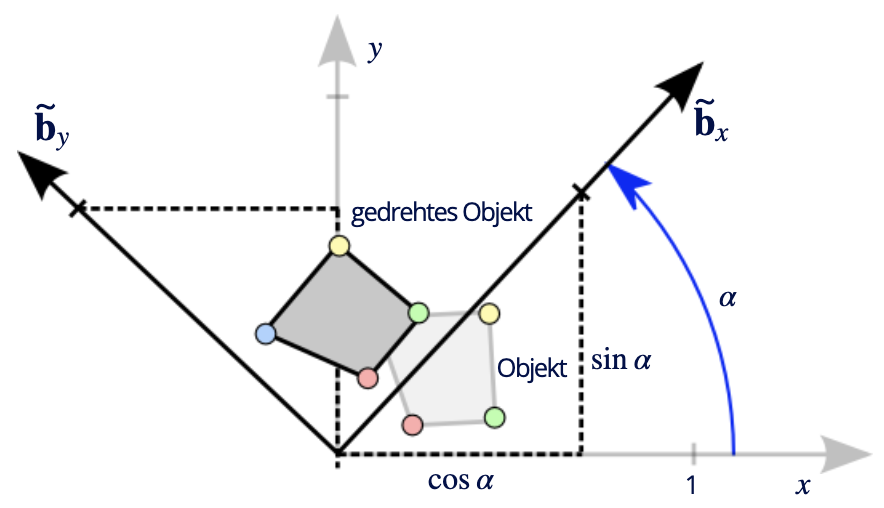
2D-Rotation

• Idee: Rotation des Koordinatensystems und anschließend Zeichnung des unveränderten Objektes in neuem Koordinatensystem

• hierfür: Wie bilden sich die neuen Koordinatenachsen auf die alten ab.

  $\begin{array}{c}{\tilde{b}}_x=\left(\begin{array}{c}\cos \alpha \\ \sin \alpha \end{array}\right)\end{array}$$\tilde b_x = \begin{pmatrix} \cos\alpha\\ \sin\alpha \end{pmatrix}$​ und $\begin{array}{c}{\tilde{b}}_y=\left(\begin{array}{c}-\sin \alpha \\ \cos \alpha \end{array}\right)\end{array}$$\tilde b_y = \begin{pmatrix} -\sin\alpha\\ \cos\alpha \end{pmatrix}$

• Es ergeben sich damit die Koordinaten des rotierten Punktes:

  $\tilde{p}={\tilde{b}}_x\ast x+{\tilde{b}}_y\ast y$$\tilde p = \tilde b_x * x+ \tilde b_y * y$

  mit Rotationsmatrix $\begin{array}{c}R=[{\tilde{b}}_x{\tilde{b}}_y]=\left[\begin{array}{cc}cos\alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]\end{array}$$R = [\tilde b_x\ \tilde b_y] = \begin{bmatrix} cos\alpha & -\sin\alpha\\ \sin\alpha & \cos\alpha \end{bmatrix}$​

  also: $\begin{array}{c}\tilde{p}=\left[\begin{array}{cc}cos\alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]\ast p\end{array}$$\tilde p = \begin{bmatrix} cos\ \alpha & -\sin\ \alpha\\ \sin\ \alpha & \cos\ \alpha \end{bmatrix} * p$​

Kombination der Transformationen

• Beispiel: erst skalieren, dann rotieren, schließlich translieren

  $\tilde{p}=R\ast s\ast p+t$$\tilde p = R * s * p + t$

Linearkombination

• Vektoren lassen sich als Linearkombination von Basisvektoren darstellen:

  $v=\sum _{i=1}^n{a}_i\ast v_i$$v = \sum_{i=1}^{n}a_i*v_i$ mit Basisvektoren $v_i$$v_i$

• Basisvektoren sind die linear unabhängigen Vektoren, die nötig sind, um alle Vektoren einer Dimension (= Anzahl der Basisvektoren) beschreiben zu können

• linear unabhängig = nicht durch Linearkombination anderer Vektoren beschreibbar
• z.B. für $R³$$R³$ üblicherweise: $\begin{array}{c}v=\alpha \ast \left(\begin{array}{c}1\\ 0\\ 0\end{array}\right)+\beta \ast \left(\begin{array}{c}0\\ 1\\ 0\end{array}\right)+\gamma \ast \left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)\end{array}$$v= \alpha * \begin{pmatrix}1\\0\\0\end{pmatrix} + \beta * \begin{pmatrix}0\\1\\0\end{pmatrix} + \gamma * \begin{pmatrix}0\\0\\1\end{pmatrix}$

• Es kann somit eine Transformationsmatrix durch eine Linearkombination der Basisvektoren erzeugt werden

Homogene Koordinaten

• Motivation: Translation ebenfalls als lineare Abbildung bzw. durch Matrixmultiplikation realisieren

• Vektoren erhalten zusätzliche Komponente (eine Dimension höher):

  $\begin{array}{c}p\in \mathbb{R}²\Rightarrow \underset{―}{p}=\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)\end{array}$$p \in \R² \Rightarrow \underline p = \begin{pmatrix}x\\y\\1\end{pmatrix}$

• translatierter Punkt:

  $\begin{array}{c}\underset{―}{\tilde{p}}=\left(\begin{array}{c}\tilde{x}\\ \tilde{y}\\ 1\end{array}\right)=\left[\begin{array}{ccc}{m}_{11}& m_{12}& t_x\\ m_{21}& m_{22}& t_y\\ 0& 0& 1\end{array}\right]\ast \left(\begin{array}{c}x\\ y\\ 1\end{array}\right)\end{array}$$\underline{\tilde p} = \begin{pmatrix}\tilde x \\ \tilde y \\ 1\end{pmatrix} = \begin{bmatrix}m_{11} & m_{12} & t_x \\ m_{21} & m_{22} & t_y \\ 0 & 0 & 1\end{bmatrix} * \begin{pmatrix}x \\ y \\1\end{pmatrix}$

  mit Rotations-/Skalierungsmatrix $\left[\begin{array}{cc}{m}_{11}& m_{12}\\ m_{21}& m_{22}\end{array}\right]$$\begin{bmatrix}m_{11} & m_{12}\\ m_{21} & m_{22} \end{bmatrix}$

• nur durch die Hinzunahme der weiteren Dimension wird die Matrixmultiplikation mathematisch möglich

• Anmerkung: Skalierung der homogenen Koordinaten hat keine Auswirkung auf dessen kartesische Koordinaten

  $\begin{array}{c}\lambda \ast \underset{―}{p}=\left(\begin{array}{c}\lambda \ast u\\ \lambda \ast v\\ \lambda \ast w\end{array}\right)\in {\mathbb{H}}^2\to p=\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}\frac{\lambda \ast u}{\lambda \ast w}\\ \frac{\lambda \ast v}{\lambda \ast w}\end{array}\right)=\left(\begin{array}{c}\frac{u}{w}\\ \frac{v}{w}\end{array}\right)\in {\mathbb{R}}^2\end{array}$$\lambda * \underline p = \begin{pmatrix}\lambda * u \\ \lambda * v \\ \lambda * w \end{pmatrix} \in \H^2 \rightarrow p = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} {\lambda * u}\over{\lambda * w} \\ {\lambda * v}\over{\lambda * w}\end{pmatrix} = \begin{pmatrix} u\over w \\ v\over w\end{pmatrix} \in \R^2$

  

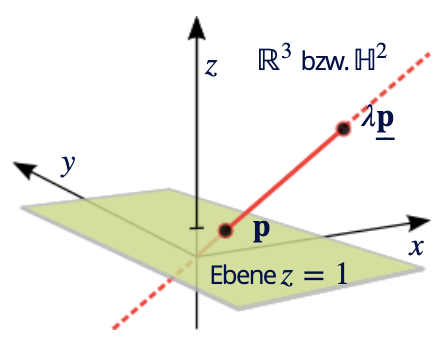
  Damit entspricht jedes Element aus ${\mathbb{R}}^2$$\R^2$ einer Geraden im ${\mathbb{H}}^2$$\H^2$

• Bei diversen Transformationen hintereinander können diese alle im homogenen Raum durchgeführt werden und das Ergebnis erst zum Schluss per Division durch die letzte Koordinate (w) auf den karthesischen (euklidischen) Raum rücktransformiert werden.

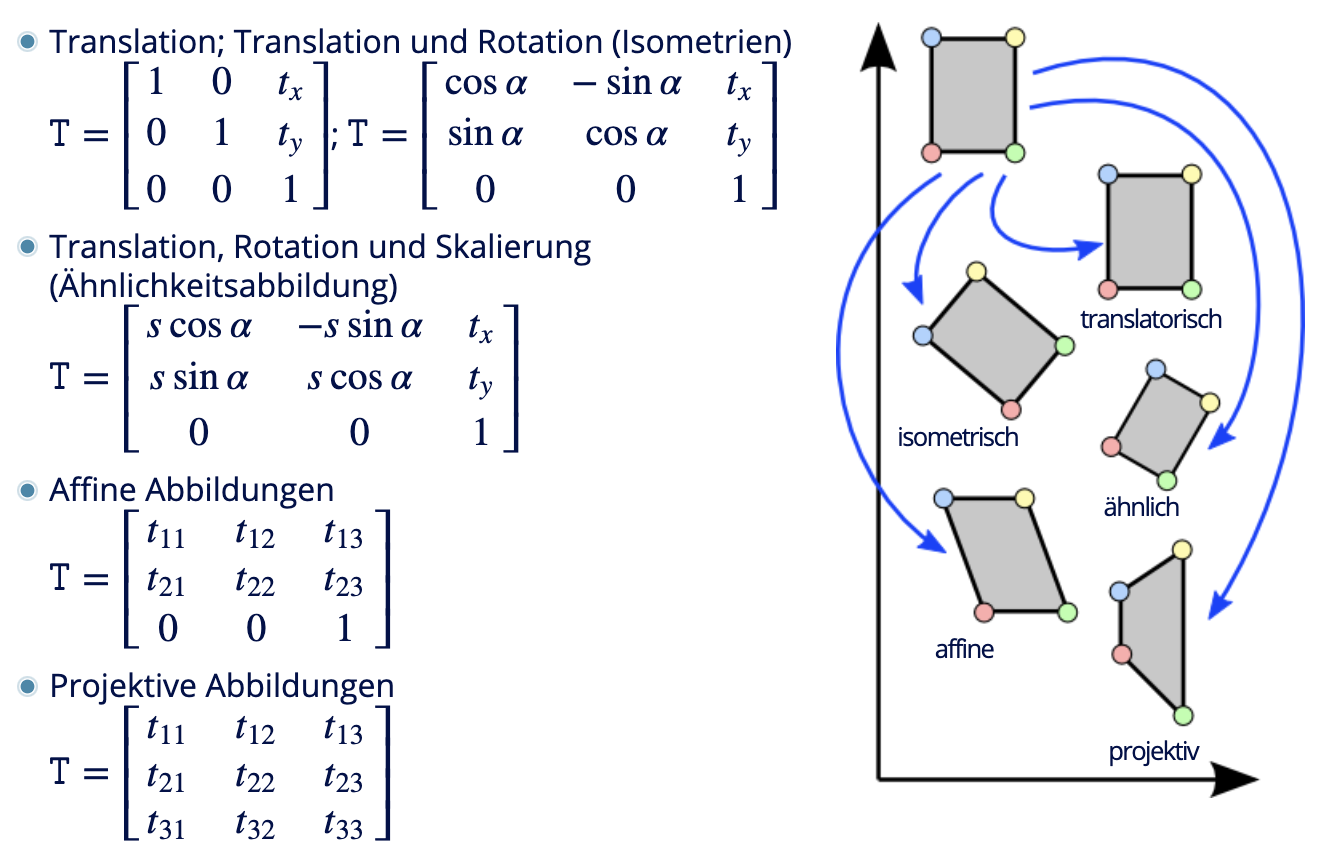
Klassifizierung von Transformationen