# Bildsynthese
## Vulkan Ray-Tracing-Pipeline *(2 Fragen)*
### Shader-Übersicht
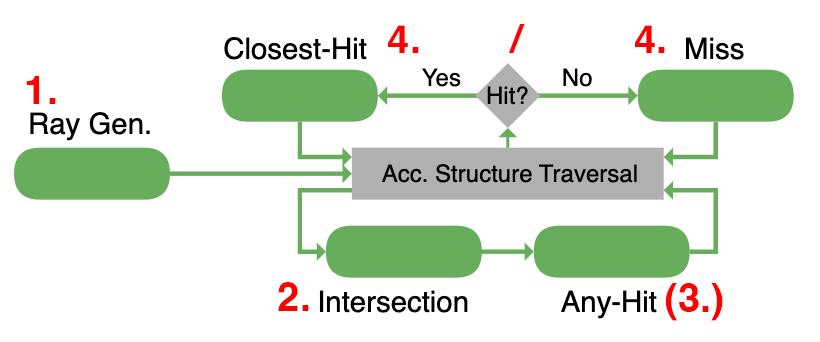 - **Ray Generation Shader**
- erstellt Strahlen und sendet sie durch `traceRayEXT(...)`
- nicht programmierbar
- `payload` enthält Informationen des Strahls
- nach abgeschlossener Strahlverfolgung wird `payload` ausgewertet
- **Intersection Shader**
- wird aufgerufen, wenn **Schnittpunkt Stahl mit Bounding-Box/Dreiecksnetz** erkannt wird.
- kann Daten in `payload` schreiben
- für Dreiecksnetz bereits vorimplementiert
- liefert **baryzentrische Koordinaten** (genaue Koordinaten innerhalb eines Dreiecks)
- **Any-Hit Shader**
- **optional, *wenn implementiert:*** aufgerufen nach Intersection Shader
- bestimmt, ob Treffer gewertet oder ignoriert *(Strahlverfolgung abgebrochen)* wird *(z.B. Blätter bei Bäumen)*
- **Closest-Hit Shader**
- wird beim **ersten Treffer** eines Stahls aufgerufen *(nach Intersection Shader)*
- falls kein Treffer $\rightarrow$ **Miss Shader**
- kann `payload` manipulieren
- kann rekursiv weitere Strahlen erzeugen *(z.B.: Senden von Schatten-Strahlen)*
- **Miss Shader**
- wird aufgerufen, falls **kein Primitiv getroffen** wird
- kann `payload` manipulieren *(z.B. Setzen der Hintergrundfarbe)*
### TLAS (top layer acceleration structure) und BLAS (bottom layer acceleration structure)
- **Ray Generation Shader**
- erstellt Strahlen und sendet sie durch `traceRayEXT(...)`
- nicht programmierbar
- `payload` enthält Informationen des Strahls
- nach abgeschlossener Strahlverfolgung wird `payload` ausgewertet
- **Intersection Shader**
- wird aufgerufen, wenn **Schnittpunkt Stahl mit Bounding-Box/Dreiecksnetz** erkannt wird.
- kann Daten in `payload` schreiben
- für Dreiecksnetz bereits vorimplementiert
- liefert **baryzentrische Koordinaten** (genaue Koordinaten innerhalb eines Dreiecks)
- **Any-Hit Shader**
- **optional, *wenn implementiert:*** aufgerufen nach Intersection Shader
- bestimmt, ob Treffer gewertet oder ignoriert *(Strahlverfolgung abgebrochen)* wird *(z.B. Blätter bei Bäumen)*
- **Closest-Hit Shader**
- wird beim **ersten Treffer** eines Stahls aufgerufen *(nach Intersection Shader)*
- falls kein Treffer $\rightarrow$ **Miss Shader**
- kann `payload` manipulieren
- kann rekursiv weitere Strahlen erzeugen *(z.B.: Senden von Schatten-Strahlen)*
- **Miss Shader**
- wird aufgerufen, falls **kein Primitiv getroffen** wird
- kann `payload` manipulieren *(z.B. Setzen der Hintergrundfarbe)*
### TLAS (top layer acceleration structure) und BLAS (bottom layer acceleration structure)
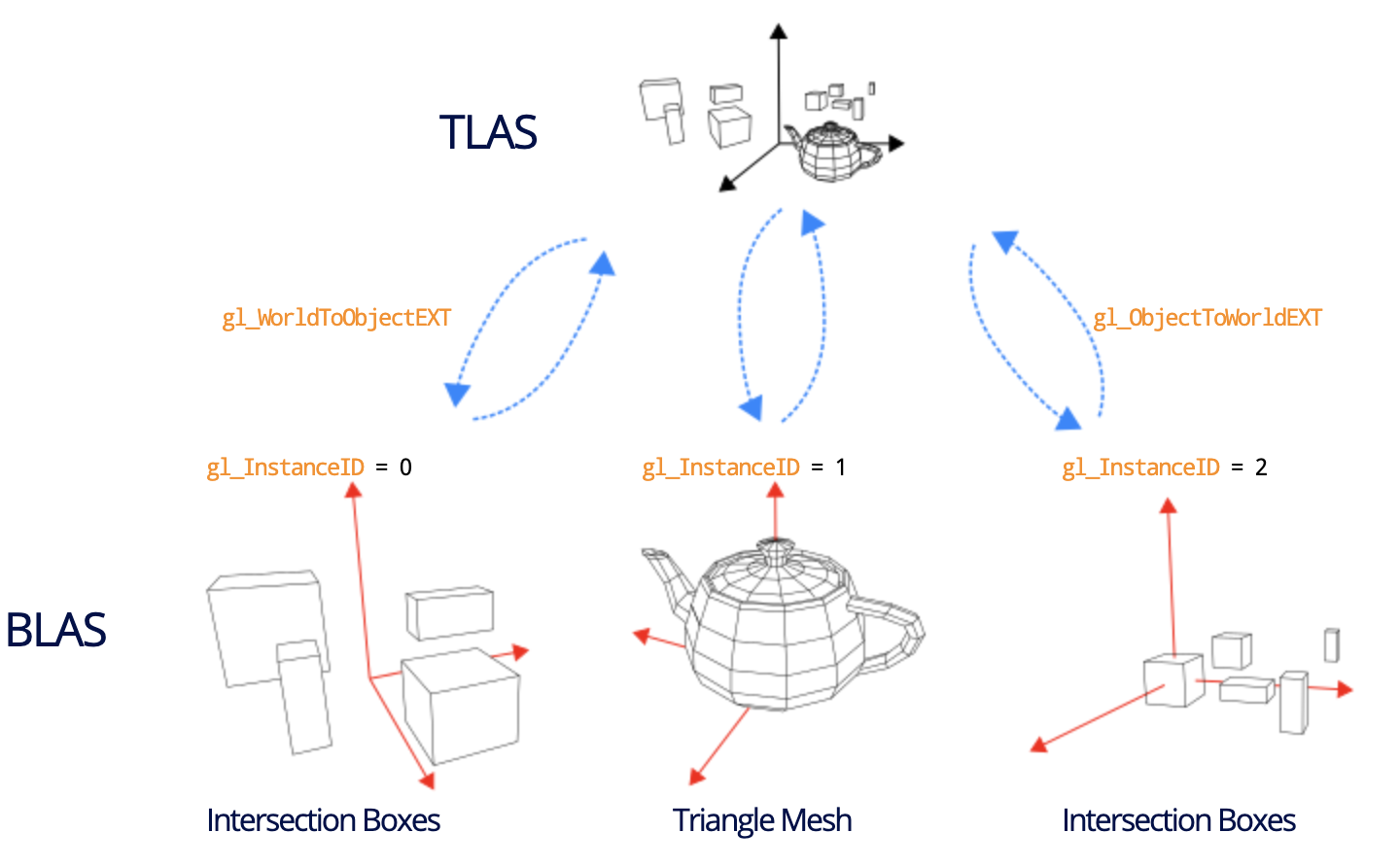 - **BLAS** sind entweder Dreiecksnetze oder Menge an **AABBs** *(axis aligned bounding boxes)*
- BLAS hat `gl_InstanceID` *(gesamtes Objekt)*
- `gl_PrimitiveID` *(konkretes Dreieck bzw. einzelte AABB)*
- jedes **BLAS** hat **Transformation von Welt- in Objektkoordinatensystem *(bzw. umgekehrt)***
### Reflexionen
- Strahldichte an einem Punkt = Summe aus **direktem Licht der Lichtquelle** und **Strahldichte durch reflektierten Strahl**
- **Reflextionsgesetz:** Einfallswinkel = Reflextionswinkel
- Ray-Tracing bricht nur ab, wenn Oberfläche nicht reflexiv, daher **Wiederholungen beschränken**
### Distributed Ray-Tracing
### Anti-Aliasing
- Versenden von **mehreren Strahlen pro Pixel**
- gleichverteilte **Zufälligkeit der Unterposition** innerhalb des Pixels
- **Halton-Sequenz:** Verhindert wiederholte Abtastung der gleichen Position
- **Hammersley-Sequenz:** effizienter als Halton, wenn Abtastwert im Vorfeld bekannt
- **Mittelung der Einflüsse** der einzelnen Strahlen
#### Soft Shadows
- Ansatz: Position der Lichtquelle wird zufällig (gleichverteilt) variiert $\rightarrow$ **Flächenlichtquelle**
## Intersection Shader *(2 Fragen)*
- Schnittpunkt kann auch im **Objektkoordinatensystem** berechnet werden ***(effizienter)***
- Ansatz: Statt Objekt in Welt- wird **Strahl in Objektkoordinatensystem transformiert**
- funktioniert, weil: Parameter `t` bleibt gleich bei parametrisiertem Strahl in Welt- und Objektkoordinatensystem
- `t` = Länge von Ursprung des Strahls zu Ein-/Austrittsschnittpunkt mit Objekt
- **Wichtig:** Bei Transformationen die **Skalierungen** enthalten, funktioniert der Ansatz nur, weil transformierter Richtungsvektor **von der Ray Tracing Pipeline nicht auf die Länge 1 normiert** wird.
Daher `gl_ObjectRayDirectionEXT` nicht im Intersection Shader normieren!
(Strahl = $s + t * r$)
### Schnittpunkt Strahl mit Kugel
- Kugelgleichung + Strahlgleichtung: Schnittpunktermittlung mittels **pq-Formel**
### Schnittpunkt Strahl mit AABB
- **Slab**-Methode: **Slab *(= Intervall in eine Raumrichtung)*** wird von zwei parallelen Ebenen begrenzt
- es kann geprüft werden, ob und wenn ja, in welchem Slab ein Schnittpunkt aufgetreten ist
- kein, ein oder zwei Schnittpunkte pro Intervall
- Strahlgleichung: $p = s + t * r$
- mit $s$ = Strahlursprung, $t$ = Stahllänge, $r$ = Strahlrichtung
### Schnittpunkt Strahl mit Dreieck
- Prüfung, ob Schnittpunkt Strahl mit Dreiecks-Ebene
- Dreieck wird durch Ebenengleichung dargestellt: $x(w, u, v)=wa+ub+vc$ mit $w=(1-u-v)$
- $w, u, v$ sind **baryzentrische Koordinaten**
- wenn $w, u, v > 0$: Punkt $x(w, u, v)$ liegt innerhalb des Dreiecks
### Baryzentrische Koordinaten
- Punkt $x(w, u, v)$ teilt Dreieck in 3 **Unterdreiecke**
- baryzentrische Koordinate: **Verhältnis** von Fläche des **gegenüberliegenden Unterdreiecks** zu **Gesamtfläche**
- **BLAS** sind entweder Dreiecksnetze oder Menge an **AABBs** *(axis aligned bounding boxes)*
- BLAS hat `gl_InstanceID` *(gesamtes Objekt)*
- `gl_PrimitiveID` *(konkretes Dreieck bzw. einzelte AABB)*
- jedes **BLAS** hat **Transformation von Welt- in Objektkoordinatensystem *(bzw. umgekehrt)***
### Reflexionen
- Strahldichte an einem Punkt = Summe aus **direktem Licht der Lichtquelle** und **Strahldichte durch reflektierten Strahl**
- **Reflextionsgesetz:** Einfallswinkel = Reflextionswinkel
- Ray-Tracing bricht nur ab, wenn Oberfläche nicht reflexiv, daher **Wiederholungen beschränken**
### Distributed Ray-Tracing
### Anti-Aliasing
- Versenden von **mehreren Strahlen pro Pixel**
- gleichverteilte **Zufälligkeit der Unterposition** innerhalb des Pixels
- **Halton-Sequenz:** Verhindert wiederholte Abtastung der gleichen Position
- **Hammersley-Sequenz:** effizienter als Halton, wenn Abtastwert im Vorfeld bekannt
- **Mittelung der Einflüsse** der einzelnen Strahlen
#### Soft Shadows
- Ansatz: Position der Lichtquelle wird zufällig (gleichverteilt) variiert $\rightarrow$ **Flächenlichtquelle**
## Intersection Shader *(2 Fragen)*
- Schnittpunkt kann auch im **Objektkoordinatensystem** berechnet werden ***(effizienter)***
- Ansatz: Statt Objekt in Welt- wird **Strahl in Objektkoordinatensystem transformiert**
- funktioniert, weil: Parameter `t` bleibt gleich bei parametrisiertem Strahl in Welt- und Objektkoordinatensystem
- `t` = Länge von Ursprung des Strahls zu Ein-/Austrittsschnittpunkt mit Objekt
- **Wichtig:** Bei Transformationen die **Skalierungen** enthalten, funktioniert der Ansatz nur, weil transformierter Richtungsvektor **von der Ray Tracing Pipeline nicht auf die Länge 1 normiert** wird.
Daher `gl_ObjectRayDirectionEXT` nicht im Intersection Shader normieren!
(Strahl = $s + t * r$)
### Schnittpunkt Strahl mit Kugel
- Kugelgleichung + Strahlgleichtung: Schnittpunktermittlung mittels **pq-Formel**
### Schnittpunkt Strahl mit AABB
- **Slab**-Methode: **Slab *(= Intervall in eine Raumrichtung)*** wird von zwei parallelen Ebenen begrenzt
- es kann geprüft werden, ob und wenn ja, in welchem Slab ein Schnittpunkt aufgetreten ist
- kein, ein oder zwei Schnittpunkte pro Intervall
- Strahlgleichung: $p = s + t * r$
- mit $s$ = Strahlursprung, $t$ = Stahllänge, $r$ = Strahlrichtung
### Schnittpunkt Strahl mit Dreieck
- Prüfung, ob Schnittpunkt Strahl mit Dreiecks-Ebene
- Dreieck wird durch Ebenengleichung dargestellt: $x(w, u, v)=wa+ub+vc$ mit $w=(1-u-v)$
- $w, u, v$ sind **baryzentrische Koordinaten**
- wenn $w, u, v > 0$: Punkt $x(w, u, v)$ liegt innerhalb des Dreiecks
### Baryzentrische Koordinaten
- Punkt $x(w, u, v)$ teilt Dreieck in 3 **Unterdreiecke**
- baryzentrische Koordinate: **Verhältnis** von Fläche des **gegenüberliegenden Unterdreiecks** zu **Gesamtfläche**
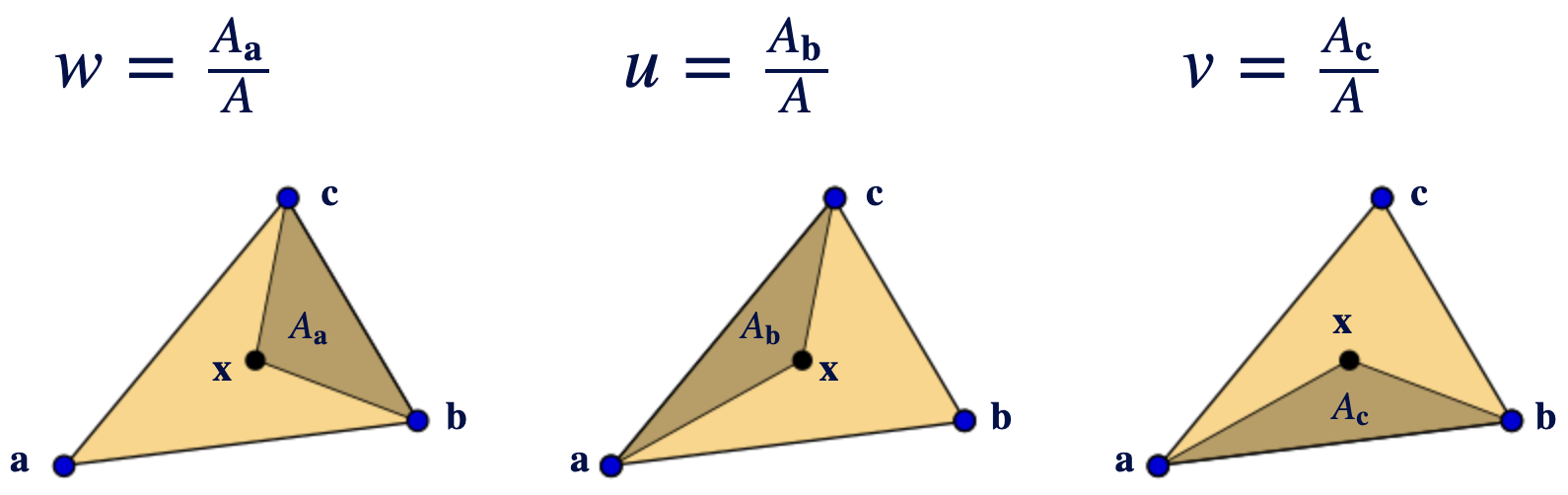 - werden genutzt, um Vertex-Daten zu **interpolieren** *(z.B. Farbe, Texturkoordinaten)*
### CSG (Constructive Solid Geometry)
- werden genutzt, um Vertex-Daten zu **interpolieren** *(z.B. Farbe, Texturkoordinaten)*
### CSG (Constructive Solid Geometry)
 ## Rendering Gleichung
- berechnet die reflektierte Strahldichte $L_o (v)$ im Oberflächenpunkt $x$ mit Normalen $n$ in Richtung $v$
- wie strahlt das Licht an einem bestimmten Punkt in eine bestimmte Richtung zurück
- $ausgehende\ Strahldichte = selbst\ emittiert + \int{BRDF,\ eingehende\ Strahldichte}$
- $L_O(v) = L_e(v) + \int_{\Omega}f_r(v,l)\ \underbrace{L_i(l)\ cos(\Theta)d\omega}_{dE(l)}$
- $L_O(v) \rightarrow$ ausgehende Strahldichte
- $L_e(v) \rightarrow$ von Fläche selbst emittierte Strahldichte
- $L_i(l) \rightarrow$ eingehende Strahldichte
- $E(l) \rightarrow$ Bestrahlungsstärke
- $f_r(v,l) \rightarrow$ BRDF
- $\Omega \rightarrow$ Gesamtheit aller Winkel der Hemisphäre über der Oberfläche
### Raumwinkel
- Dreidimensionales Gegenstück zum 2D-Winkel
- Raumwinkel $\Omega$ einer Fläche $A$ entspricht **Quotienten** der Fläche $S$, wenn $A$ auf eine Kugel vom Radius $r$ projiziert wird
- $\Omega = {S \over r^2}$
- Bei konstanter Größe nimmt der Raumwinkel einer Fläche quadratisch mit dem Abstand vom Zentrum ab
- Einheit **Steradiant** (sr)
### Strahlungsfluss
- Strahlungsfluss $\Phi$ = **Strahlungsenergie pro Zeit**
- Summe der Photonen-Energien, die pro Zeitraum $\Delta t$ emittiert werden
- Einheit: **Watt**
### Strahlstärke
- Strahlstärke $I$= **Strahlungsfluss pro Raumwinkel**
- Summe der Photonen-Energien die pro **Zeit und Raumwinkel** emittiert werden
- Wird benötigt, wenn Lichtquelle beispielsweise nicht in alle Richtungen gleich stark abstrahlt
- Einheit: **Watt pro Steradiant**
### Bestrahlungsstärke
- Bestrahlungsstärke $E$ = **Strahlungsfluss pro Flächenelement**
- einfallende Photonen-Energie **pro Zeit pro Flächenelement**
- Strahlungsfluss kommt aus allen Richtungen der Hemisphäre über der Fläche
- Einheit **Watt pro Quadratmeter**
### Strahldichte
- Strahldichte $L$ = **Strahlungsfluss pro Raumwinkel und sichtbarer Fläche**
- Strahlungsfluss in Richtung Auge
- Entspricht beobachteter Helligkeit
- Einheit: **Watt pro Steradiant pro Quadratmeter**
### BRDF (Bidirectional Reflection Distribution Function)
- Beschreibt den **winkelabhängigen spektralen Reflexionsfaktor einer Oberfläche** durch das Verhältnis von **reflektierter Strahldichte $L_o$** zur **einfallenden Bestrahlungsstärke $E$**
- $f_r(v,l)$
- $v \rightarrow$ ausgehende Richtung
- $l \rightarrow$ eingehende Richtung
- $v$ und $l$ können mit Winkeln parametrisiert werden
- 4-dimensionale Funktion, welche die **Reflexionseigenschaften einer Fläche** sehr genau beschreiben
- Reflexionseigenschaften sind in Materialdatenbanken (4D-Tabellen) abgelegt
- Da 4D-Tabellen viel Speicher benötigen und Materialien sich nicht direkt editieren lassen $\rightarrow$ Verwendung von parametrischen BRDF-Modellen (Phong, Blinn-Phong, Cook-Torrance, etc)
#### BRDF Eigenschaften
- Immer positiv
- **Helmholtz Reziprozität $\rightarrow$** eingehende und ausgehende Richtung können vertauscht werden
- Energieerhaltung ist $\leq 1$
## Path Tracing
- Ziel: **Effizientes, optisch korrektes Approximieren der Rendering Gleichung**
- Ansatz: Weiterverfolgung **nur eines zufälligen Strahls**
- nicht alle Punkte gleichermaßen berechnen, sondern priorisiert die, die den größten optischen Einfluss haben $\rightarrow$ *abhängig von passender WDF*
- Erste Möglichkeit: Approximation mittels Riemann-Summe
- Integral wird in Summenformel umgewandelt
- immernoch **ineffizient, da gleichförmige Abtastung**
### Importance Sampling
- Durch **Importance Sampling Theorie** kann jedes Integral auch durch eine Summe approximiert werden
- benutzt beliebige **Wahrscheinlichkeitsdichtefunktion** (WDF), welche die Bedingung $\int_a^b p(x) dx = 1$ erfüllen muss
- beste WDF wäre, wenn diese der Form der Funktion folgt
- $p(x)=\int_a^b{f(x)}$
- Dichte sollte höher sein, wenn Funktionswerte höher sind
- **verhindert Spikes**
- **Inversionsmethode**
- Ziel: Möglichst gutes Ergebnis nach wenig Abtastwerten $\rightarrow$ WDF so wählen, dass sie Form der Funktion folgt
- Ermöglicht die Erzeugung von **Zufallszahlen nach WDF (nicht linear) aus gleichverteilten Zufallszahlen**
### Auswerten der Rendering-Gleichung
- Problem bisherigen Ansatzes
- rekursive Strahlverfolgung **bei diffuser BRDF und kleiner Lichtquelle** ineffizient/qualitativ schlecht
- Beitrag nur dann, wenn Strahl Lichtquelle trifft
## Rendering Gleichung
- berechnet die reflektierte Strahldichte $L_o (v)$ im Oberflächenpunkt $x$ mit Normalen $n$ in Richtung $v$
- wie strahlt das Licht an einem bestimmten Punkt in eine bestimmte Richtung zurück
- $ausgehende\ Strahldichte = selbst\ emittiert + \int{BRDF,\ eingehende\ Strahldichte}$
- $L_O(v) = L_e(v) + \int_{\Omega}f_r(v,l)\ \underbrace{L_i(l)\ cos(\Theta)d\omega}_{dE(l)}$
- $L_O(v) \rightarrow$ ausgehende Strahldichte
- $L_e(v) \rightarrow$ von Fläche selbst emittierte Strahldichte
- $L_i(l) \rightarrow$ eingehende Strahldichte
- $E(l) \rightarrow$ Bestrahlungsstärke
- $f_r(v,l) \rightarrow$ BRDF
- $\Omega \rightarrow$ Gesamtheit aller Winkel der Hemisphäre über der Oberfläche
### Raumwinkel
- Dreidimensionales Gegenstück zum 2D-Winkel
- Raumwinkel $\Omega$ einer Fläche $A$ entspricht **Quotienten** der Fläche $S$, wenn $A$ auf eine Kugel vom Radius $r$ projiziert wird
- $\Omega = {S \over r^2}$
- Bei konstanter Größe nimmt der Raumwinkel einer Fläche quadratisch mit dem Abstand vom Zentrum ab
- Einheit **Steradiant** (sr)
### Strahlungsfluss
- Strahlungsfluss $\Phi$ = **Strahlungsenergie pro Zeit**
- Summe der Photonen-Energien, die pro Zeitraum $\Delta t$ emittiert werden
- Einheit: **Watt**
### Strahlstärke
- Strahlstärke $I$= **Strahlungsfluss pro Raumwinkel**
- Summe der Photonen-Energien die pro **Zeit und Raumwinkel** emittiert werden
- Wird benötigt, wenn Lichtquelle beispielsweise nicht in alle Richtungen gleich stark abstrahlt
- Einheit: **Watt pro Steradiant**
### Bestrahlungsstärke
- Bestrahlungsstärke $E$ = **Strahlungsfluss pro Flächenelement**
- einfallende Photonen-Energie **pro Zeit pro Flächenelement**
- Strahlungsfluss kommt aus allen Richtungen der Hemisphäre über der Fläche
- Einheit **Watt pro Quadratmeter**
### Strahldichte
- Strahldichte $L$ = **Strahlungsfluss pro Raumwinkel und sichtbarer Fläche**
- Strahlungsfluss in Richtung Auge
- Entspricht beobachteter Helligkeit
- Einheit: **Watt pro Steradiant pro Quadratmeter**
### BRDF (Bidirectional Reflection Distribution Function)
- Beschreibt den **winkelabhängigen spektralen Reflexionsfaktor einer Oberfläche** durch das Verhältnis von **reflektierter Strahldichte $L_o$** zur **einfallenden Bestrahlungsstärke $E$**
- $f_r(v,l)$
- $v \rightarrow$ ausgehende Richtung
- $l \rightarrow$ eingehende Richtung
- $v$ und $l$ können mit Winkeln parametrisiert werden
- 4-dimensionale Funktion, welche die **Reflexionseigenschaften einer Fläche** sehr genau beschreiben
- Reflexionseigenschaften sind in Materialdatenbanken (4D-Tabellen) abgelegt
- Da 4D-Tabellen viel Speicher benötigen und Materialien sich nicht direkt editieren lassen $\rightarrow$ Verwendung von parametrischen BRDF-Modellen (Phong, Blinn-Phong, Cook-Torrance, etc)
#### BRDF Eigenschaften
- Immer positiv
- **Helmholtz Reziprozität $\rightarrow$** eingehende und ausgehende Richtung können vertauscht werden
- Energieerhaltung ist $\leq 1$
## Path Tracing
- Ziel: **Effizientes, optisch korrektes Approximieren der Rendering Gleichung**
- Ansatz: Weiterverfolgung **nur eines zufälligen Strahls**
- nicht alle Punkte gleichermaßen berechnen, sondern priorisiert die, die den größten optischen Einfluss haben $\rightarrow$ *abhängig von passender WDF*
- Erste Möglichkeit: Approximation mittels Riemann-Summe
- Integral wird in Summenformel umgewandelt
- immernoch **ineffizient, da gleichförmige Abtastung**
### Importance Sampling
- Durch **Importance Sampling Theorie** kann jedes Integral auch durch eine Summe approximiert werden
- benutzt beliebige **Wahrscheinlichkeitsdichtefunktion** (WDF), welche die Bedingung $\int_a^b p(x) dx = 1$ erfüllen muss
- beste WDF wäre, wenn diese der Form der Funktion folgt
- $p(x)=\int_a^b{f(x)}$
- Dichte sollte höher sein, wenn Funktionswerte höher sind
- **verhindert Spikes**
- **Inversionsmethode**
- Ziel: Möglichst gutes Ergebnis nach wenig Abtastwerten $\rightarrow$ WDF so wählen, dass sie Form der Funktion folgt
- Ermöglicht die Erzeugung von **Zufallszahlen nach WDF (nicht linear) aus gleichverteilten Zufallszahlen**
### Auswerten der Rendering-Gleichung
- Problem bisherigen Ansatzes
- rekursive Strahlverfolgung **bei diffuser BRDF und kleiner Lichtquelle** ineffizient/qualitativ schlecht
- Beitrag nur dann, wenn Strahl Lichtquelle trifft
 - **Lösung**: Aufteilen der Rendering-Gleichung in **direkten und indirekten Anteil**
- direkter Anteil: **direkter Beitrag der Lichtquelle** *(Überprüfung mittels Schattenstrahl)*
- nicht mehr über kompletten Halbraum integrieren, sondern **nur über Raumwinkel der Lichtquelle**
- indirekter Anteil: Weiterverfolgen **zufälliger Richtung im Halbraum**
- Beitrag von direkter Lichtquelle hier verwerfen, um ihn nicht doppelt zu zählen
## PBR (physically-based Rendering) Materialen
- Materialen werden beschrieben durch eine Kombination von **transmittivem, reflektivem und streuendem** *(scattering)* Anteil
- Koponenten der **BSRF**:
- BRDF Dielektrika *(R = reflection)*
- BRDF Metalle
- BTDF *(T = transmission)*
- Emission
- Klarlack (clear coat)
- Glanz (sheen)
- Subsurface scattering
### Micofacetten BRDF
- Oberfläche wird aus Microfacetten beschrieben
- **Lösung**: Aufteilen der Rendering-Gleichung in **direkten und indirekten Anteil**
- direkter Anteil: **direkter Beitrag der Lichtquelle** *(Überprüfung mittels Schattenstrahl)*
- nicht mehr über kompletten Halbraum integrieren, sondern **nur über Raumwinkel der Lichtquelle**
- indirekter Anteil: Weiterverfolgen **zufälliger Richtung im Halbraum**
- Beitrag von direkter Lichtquelle hier verwerfen, um ihn nicht doppelt zu zählen
## PBR (physically-based Rendering) Materialen
- Materialen werden beschrieben durch eine Kombination von **transmittivem, reflektivem und streuendem** *(scattering)* Anteil
- Koponenten der **BSRF**:
- BRDF Dielektrika *(R = reflection)*
- BRDF Metalle
- BTDF *(T = transmission)*
- Emission
- Klarlack (clear coat)
- Glanz (sheen)
- Subsurface scattering
### Micofacetten BRDF
- Oberfläche wird aus Microfacetten beschrieben
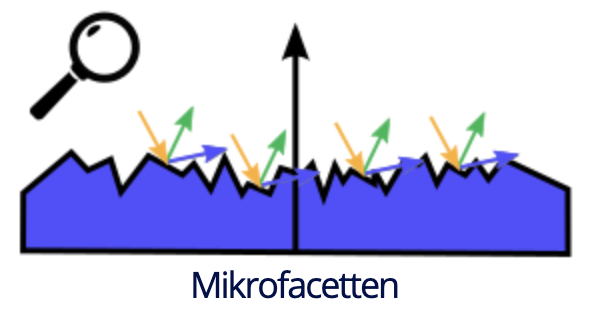 - zusammengesetzt aus **diffusem** *(konsant)*
- und **spekularem** Anteil
- **Fresnel**-Reflexionsgrad
- Verteilung der Microfacetten ***(Rauheit)***
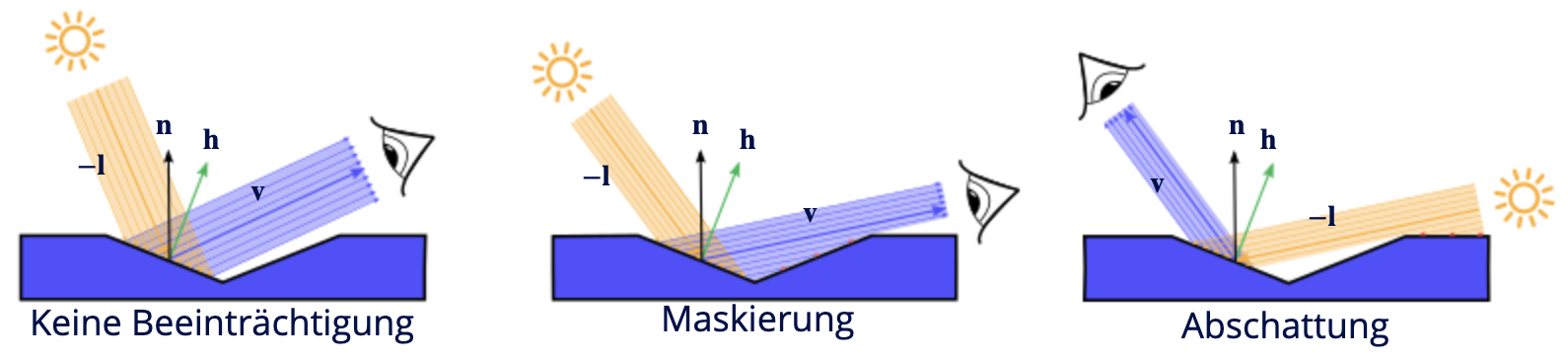
- Geometriefaktor ***(Selbstbeschattung)***
- zusammengesetzt aus **diffusem** *(konsant)*
- und **spekularem** Anteil
- **Fresnel**-Reflexionsgrad
- Verteilung der Microfacetten ***(Rauheit)***
- Geometriefaktor ***(Selbstbeschattung)***
 ### Fresnel Reflexion
- reflexiver und transmittiever Anteil hängen von Einfallswinkel und Brechungsindex des Materials ab
- **Refraktion:** Brechung an Oberfläche
- optisch dünner $\rightarrow$ optisch dichter: Brechung zur Normalen hin
- optisch dichter $\rightarrow$ optisch dünner: Brechung von Normalen weg
- **Berechungsmöglichkeiten:** **Cook Torrance** oder **Schlick** *(Approximation, schneller)*
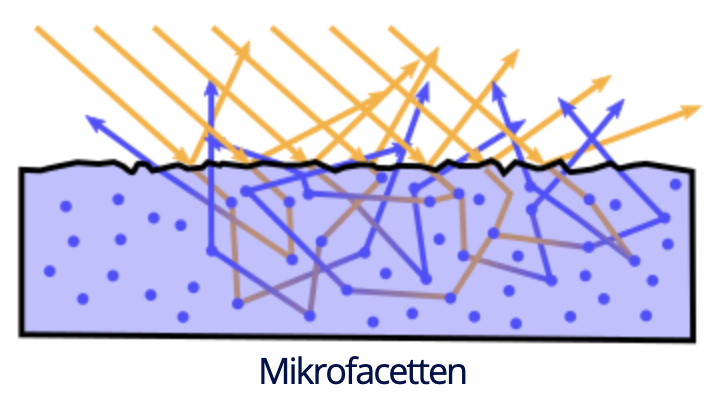
#### Fresnel Reflexion: Dielektrika
- winkelabhängig wird entweder reflektiert, transmittiert oder absorbiert
- **reflektiver Anteil** wird an Microfacetten gestreut $\rightarrow$ **spekularer Anteil** der Reflexion
- **transmittiver Anteil** wird bei opaken *(durchsichtigen)* unter der Oberfläche zufällig abgelenkt *(tlws. absorbiert)* $\rightarrow$ **diffuser Anteil** der Reflexion
- mehr Licht reflektiert $\rightarrow$ weniger Licht transmittiert $\rightarrow$ geringerer diffuser Anteil
- reflexiver und transmittiever Anteil hängen von Einfallswinkel und Brechungsindex des Materials ab
### Fresnel Reflexion
- reflexiver und transmittiever Anteil hängen von Einfallswinkel und Brechungsindex des Materials ab
- **Refraktion:** Brechung an Oberfläche
- optisch dünner $\rightarrow$ optisch dichter: Brechung zur Normalen hin
- optisch dichter $\rightarrow$ optisch dünner: Brechung von Normalen weg
- **Berechungsmöglichkeiten:** **Cook Torrance** oder **Schlick** *(Approximation, schneller)*
#### Fresnel Reflexion: Dielektrika
- winkelabhängig wird entweder reflektiert, transmittiert oder absorbiert
- **reflektiver Anteil** wird an Microfacetten gestreut $\rightarrow$ **spekularer Anteil** der Reflexion
- **transmittiver Anteil** wird bei opaken *(durchsichtigen)* unter der Oberfläche zufällig abgelenkt *(tlws. absorbiert)* $\rightarrow$ **diffuser Anteil** der Reflexion
- mehr Licht reflektiert $\rightarrow$ weniger Licht transmittiert $\rightarrow$ geringerer diffuser Anteil
- reflexiver und transmittiever Anteil hängen von Einfallswinkel und Brechungsindex des Materials ab
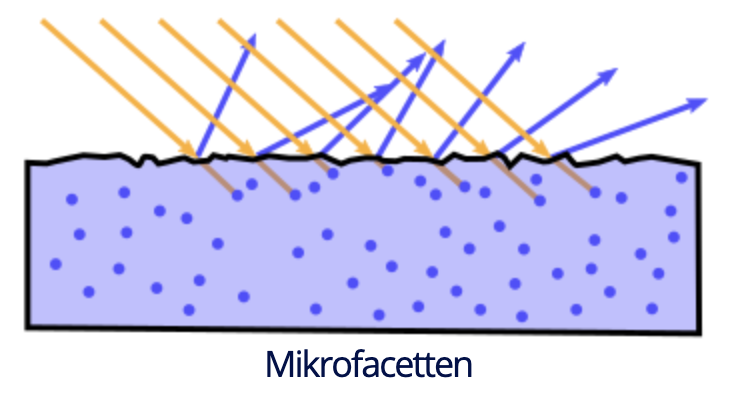
 #### Fresnel Reflexion: Metalle
- transmittiver Anteil wird absorbiert $\rightarrow$ **keine diffuse Reflexion**
- **spekularer Anteil** ist **farbig**, da reflektierter Anteil abhängig von Wellenlänge
#### Fresnel Reflexion: Metalle
- transmittiver Anteil wird absorbiert $\rightarrow$ **keine diffuse Reflexion**
- **spekularer Anteil** ist **farbig**, da reflektierter Anteil abhängig von Wellenlänge
 ## Bildbasierte Beleuchtung
- **emmitierte Strahldichte** $L_i$ der Umgebung wird **durch sphärisches Umgebungsbild** *(Environment Map)* angegeben
- Zusammenhang zwischen Textur- und Kugelkoordinaten
### Importance Sampling der Environment Map
- Umbegungsbild wird in **Grauwertbild** $g(s,t)$ umgewandelt
- Parametrisierung in Texturkoordinaten: $s, t \in [0,1]$
- Verteilungsfunktion kann nicht invertiert werden, da nicht nach Zufallsvariable aufgelöst werden kann, daher:
- **zeilenweises** Durchlaufen, bis Zufallsvariable erreicht $\rightarrow$ Zeile, in der Abtastwert genommen wird
- **spaltenweises** Durchlaufen, bis Zufallsvariable erreicht $\rightarrow$ Abtastpunkt
## Multiple Importance Sampling
- **Problem:** Da **BRDF** druch **WDF** geteilt wird, entstehen extrem hohe Sample-Werte, wo **WDF** sehr gering $\rightarrow$ Noise
- also wenn **BRDF** bzw. $f$ **groß** und **WDF** bzw. $p$ **klein**
- grobes Prinzip: Nutzung bisherigen Durchschnitts und Erwartungswerten zur Entscheidung der Sampling-Methode
- **Ziel:** Verminderung von Noise durch Kombination verschiedener Sampling-Verfahren
- nur **BRDF**-Sampling:
- gut auf stark reflektiven Materialien
- schlecht bei matteren Materialien
- nur **Light**-Sampling
- gut auf matteren Materialien
- schlecht auf stark reflektiven Materialien
## Bildbasierte Beleuchtung
- **emmitierte Strahldichte** $L_i$ der Umgebung wird **durch sphärisches Umgebungsbild** *(Environment Map)* angegeben
- Zusammenhang zwischen Textur- und Kugelkoordinaten
### Importance Sampling der Environment Map
- Umbegungsbild wird in **Grauwertbild** $g(s,t)$ umgewandelt
- Parametrisierung in Texturkoordinaten: $s, t \in [0,1]$
- Verteilungsfunktion kann nicht invertiert werden, da nicht nach Zufallsvariable aufgelöst werden kann, daher:
- **zeilenweises** Durchlaufen, bis Zufallsvariable erreicht $\rightarrow$ Zeile, in der Abtastwert genommen wird
- **spaltenweises** Durchlaufen, bis Zufallsvariable erreicht $\rightarrow$ Abtastpunkt
## Multiple Importance Sampling
- **Problem:** Da **BRDF** druch **WDF** geteilt wird, entstehen extrem hohe Sample-Werte, wo **WDF** sehr gering $\rightarrow$ Noise
- also wenn **BRDF** bzw. $f$ **groß** und **WDF** bzw. $p$ **klein**
- grobes Prinzip: Nutzung bisherigen Durchschnitts und Erwartungswerten zur Entscheidung der Sampling-Methode
- **Ziel:** Verminderung von Noise durch Kombination verschiedener Sampling-Verfahren
- nur **BRDF**-Sampling:
- gut auf stark reflektiven Materialien
- schlecht bei matteren Materialien
- nur **Light**-Sampling
- gut auf matteren Materialien
- schlecht auf stark reflektiven Materialien - **Ray Generation Shader**
- erstellt Strahlen und sendet sie durch `traceRayEXT(...)`
- nicht programmierbar
- `payload` enthält Informationen des Strahls
- nach abgeschlossener Strahlverfolgung wird `payload` ausgewertet
- **Intersection Shader**
- wird aufgerufen, wenn **Schnittpunkt Stahl mit Bounding-Box/Dreiecksnetz** erkannt wird.
- kann Daten in `payload` schreiben
- für Dreiecksnetz bereits vorimplementiert
- liefert **baryzentrische Koordinaten** (genaue Koordinaten innerhalb eines Dreiecks)
- **Any-Hit Shader**
- **optional, *wenn implementiert:*** aufgerufen nach Intersection Shader
- bestimmt, ob Treffer gewertet oder ignoriert *(Strahlverfolgung abgebrochen)* wird *(z.B. Blätter bei Bäumen)*
- **Closest-Hit Shader**
- wird beim **ersten Treffer** eines Stahls aufgerufen *(nach Intersection Shader)*
- falls kein Treffer $\rightarrow$ **Miss Shader**
- kann `payload` manipulieren
- kann rekursiv weitere Strahlen erzeugen *(z.B.: Senden von Schatten-Strahlen)*
- **Miss Shader**
- wird aufgerufen, falls **kein Primitiv getroffen** wird
- kann `payload` manipulieren *(z.B. Setzen der Hintergrundfarbe)*
### TLAS (top layer acceleration structure) und BLAS (bottom layer acceleration structure)
- **Ray Generation Shader**
- erstellt Strahlen und sendet sie durch `traceRayEXT(...)`
- nicht programmierbar
- `payload` enthält Informationen des Strahls
- nach abgeschlossener Strahlverfolgung wird `payload` ausgewertet
- **Intersection Shader**
- wird aufgerufen, wenn **Schnittpunkt Stahl mit Bounding-Box/Dreiecksnetz** erkannt wird.
- kann Daten in `payload` schreiben
- für Dreiecksnetz bereits vorimplementiert
- liefert **baryzentrische Koordinaten** (genaue Koordinaten innerhalb eines Dreiecks)
- **Any-Hit Shader**
- **optional, *wenn implementiert:*** aufgerufen nach Intersection Shader
- bestimmt, ob Treffer gewertet oder ignoriert *(Strahlverfolgung abgebrochen)* wird *(z.B. Blätter bei Bäumen)*
- **Closest-Hit Shader**
- wird beim **ersten Treffer** eines Stahls aufgerufen *(nach Intersection Shader)*
- falls kein Treffer $\rightarrow$ **Miss Shader**
- kann `payload` manipulieren
- kann rekursiv weitere Strahlen erzeugen *(z.B.: Senden von Schatten-Strahlen)*
- **Miss Shader**
- wird aufgerufen, falls **kein Primitiv getroffen** wird
- kann `payload` manipulieren *(z.B. Setzen der Hintergrundfarbe)*
### TLAS (top layer acceleration structure) und BLAS (bottom layer acceleration structure)
 - **BLAS** sind entweder Dreiecksnetze oder Menge an **AABBs** *(axis aligned bounding boxes)*
- BLAS hat `gl_InstanceID` *(gesamtes Objekt)*
- `gl_PrimitiveID` *(konkretes Dreieck bzw. einzelte AABB)*
- jedes **BLAS** hat **Transformation von Welt- in Objektkoordinatensystem *(bzw. umgekehrt)***
### Reflexionen
- Strahldichte an einem Punkt = Summe aus **direktem Licht der Lichtquelle** und **Strahldichte durch reflektierten Strahl**
- **Reflextionsgesetz:** Einfallswinkel = Reflextionswinkel
- Ray-Tracing bricht nur ab, wenn Oberfläche nicht reflexiv, daher **Wiederholungen beschränken**
### Distributed Ray-Tracing
### Anti-Aliasing
- Versenden von **mehreren Strahlen pro Pixel**
- gleichverteilte **Zufälligkeit der Unterposition** innerhalb des Pixels
- **Halton-Sequenz:** Verhindert wiederholte Abtastung der gleichen Position
- **Hammersley-Sequenz:** effizienter als Halton, wenn Abtastwert im Vorfeld bekannt
- **Mittelung der Einflüsse** der einzelnen Strahlen
#### Soft Shadows
- Ansatz: Position der Lichtquelle wird zufällig (gleichverteilt) variiert $\rightarrow$ **Flächenlichtquelle**
## Intersection Shader *(2 Fragen)*
- Schnittpunkt kann auch im **Objektkoordinatensystem** berechnet werden ***(effizienter)***
- Ansatz: Statt Objekt in Welt- wird **Strahl in Objektkoordinatensystem transformiert**
- funktioniert, weil: Parameter `t` bleibt gleich bei parametrisiertem Strahl in Welt- und Objektkoordinatensystem
- `t` = Länge von Ursprung des Strahls zu Ein-/Austrittsschnittpunkt mit Objekt
- **Wichtig:** Bei Transformationen die **Skalierungen** enthalten, funktioniert der Ansatz nur, weil transformierter Richtungsvektor **von der Ray Tracing Pipeline nicht auf die Länge 1 normiert** wird.
Daher `gl_ObjectRayDirectionEXT` nicht im Intersection Shader normieren!
(Strahl = $s + t * r$)
### Schnittpunkt Strahl mit Kugel
- Kugelgleichung + Strahlgleichtung: Schnittpunktermittlung mittels **pq-Formel**
### Schnittpunkt Strahl mit AABB
- **Slab**-Methode: **Slab *(= Intervall in eine Raumrichtung)*** wird von zwei parallelen Ebenen begrenzt
- es kann geprüft werden, ob und wenn ja, in welchem Slab ein Schnittpunkt aufgetreten ist
- kein, ein oder zwei Schnittpunkte pro Intervall
- Strahlgleichung: $p = s + t * r$
- mit $s$ = Strahlursprung, $t$ = Stahllänge, $r$ = Strahlrichtung
### Schnittpunkt Strahl mit Dreieck
- Prüfung, ob Schnittpunkt Strahl mit Dreiecks-Ebene
- Dreieck wird durch Ebenengleichung dargestellt: $x(w, u, v)=wa+ub+vc$ mit $w=(1-u-v)$
- $w, u, v$ sind **baryzentrische Koordinaten**
- wenn $w, u, v > 0$: Punkt $x(w, u, v)$ liegt innerhalb des Dreiecks
### Baryzentrische Koordinaten
- Punkt $x(w, u, v)$ teilt Dreieck in 3 **Unterdreiecke**
- baryzentrische Koordinate: **Verhältnis** von Fläche des **gegenüberliegenden Unterdreiecks** zu **Gesamtfläche**
- **BLAS** sind entweder Dreiecksnetze oder Menge an **AABBs** *(axis aligned bounding boxes)*
- BLAS hat `gl_InstanceID` *(gesamtes Objekt)*
- `gl_PrimitiveID` *(konkretes Dreieck bzw. einzelte AABB)*
- jedes **BLAS** hat **Transformation von Welt- in Objektkoordinatensystem *(bzw. umgekehrt)***
### Reflexionen
- Strahldichte an einem Punkt = Summe aus **direktem Licht der Lichtquelle** und **Strahldichte durch reflektierten Strahl**
- **Reflextionsgesetz:** Einfallswinkel = Reflextionswinkel
- Ray-Tracing bricht nur ab, wenn Oberfläche nicht reflexiv, daher **Wiederholungen beschränken**
### Distributed Ray-Tracing
### Anti-Aliasing
- Versenden von **mehreren Strahlen pro Pixel**
- gleichverteilte **Zufälligkeit der Unterposition** innerhalb des Pixels
- **Halton-Sequenz:** Verhindert wiederholte Abtastung der gleichen Position
- **Hammersley-Sequenz:** effizienter als Halton, wenn Abtastwert im Vorfeld bekannt
- **Mittelung der Einflüsse** der einzelnen Strahlen
#### Soft Shadows
- Ansatz: Position der Lichtquelle wird zufällig (gleichverteilt) variiert $\rightarrow$ **Flächenlichtquelle**
## Intersection Shader *(2 Fragen)*
- Schnittpunkt kann auch im **Objektkoordinatensystem** berechnet werden ***(effizienter)***
- Ansatz: Statt Objekt in Welt- wird **Strahl in Objektkoordinatensystem transformiert**
- funktioniert, weil: Parameter `t` bleibt gleich bei parametrisiertem Strahl in Welt- und Objektkoordinatensystem
- `t` = Länge von Ursprung des Strahls zu Ein-/Austrittsschnittpunkt mit Objekt
- **Wichtig:** Bei Transformationen die **Skalierungen** enthalten, funktioniert der Ansatz nur, weil transformierter Richtungsvektor **von der Ray Tracing Pipeline nicht auf die Länge 1 normiert** wird.
Daher `gl_ObjectRayDirectionEXT` nicht im Intersection Shader normieren!
(Strahl = $s + t * r$)
### Schnittpunkt Strahl mit Kugel
- Kugelgleichung + Strahlgleichtung: Schnittpunktermittlung mittels **pq-Formel**
### Schnittpunkt Strahl mit AABB
- **Slab**-Methode: **Slab *(= Intervall in eine Raumrichtung)*** wird von zwei parallelen Ebenen begrenzt
- es kann geprüft werden, ob und wenn ja, in welchem Slab ein Schnittpunkt aufgetreten ist
- kein, ein oder zwei Schnittpunkte pro Intervall
- Strahlgleichung: $p = s + t * r$
- mit $s$ = Strahlursprung, $t$ = Stahllänge, $r$ = Strahlrichtung
### Schnittpunkt Strahl mit Dreieck
- Prüfung, ob Schnittpunkt Strahl mit Dreiecks-Ebene
- Dreieck wird durch Ebenengleichung dargestellt: $x(w, u, v)=wa+ub+vc$ mit $w=(1-u-v)$
- $w, u, v$ sind **baryzentrische Koordinaten**
- wenn $w, u, v > 0$: Punkt $x(w, u, v)$ liegt innerhalb des Dreiecks
### Baryzentrische Koordinaten
- Punkt $x(w, u, v)$ teilt Dreieck in 3 **Unterdreiecke**
- baryzentrische Koordinate: **Verhältnis** von Fläche des **gegenüberliegenden Unterdreiecks** zu **Gesamtfläche**
 - werden genutzt, um Vertex-Daten zu **interpolieren** *(z.B. Farbe, Texturkoordinaten)*
### CSG (Constructive Solid Geometry)
- werden genutzt, um Vertex-Daten zu **interpolieren** *(z.B. Farbe, Texturkoordinaten)*
### CSG (Constructive Solid Geometry)
 ## Rendering Gleichung
- berechnet die reflektierte Strahldichte $L_o (v)$ im Oberflächenpunkt $x$ mit Normalen $n$ in Richtung $v$
- wie strahlt das Licht an einem bestimmten Punkt in eine bestimmte Richtung zurück
- $ausgehende\ Strahldichte = selbst\ emittiert + \int{BRDF,\ eingehende\ Strahldichte}$
- $L_O(v) = L_e(v) + \int_{\Omega}f_r(v,l)\ \underbrace{L_i(l)\ cos(\Theta)d\omega}_{dE(l)}$
- $L_O(v) \rightarrow$ ausgehende Strahldichte
- $L_e(v) \rightarrow$ von Fläche selbst emittierte Strahldichte
- $L_i(l) \rightarrow$ eingehende Strahldichte
- $E(l) \rightarrow$ Bestrahlungsstärke
- $f_r(v,l) \rightarrow$ BRDF
- $\Omega \rightarrow$ Gesamtheit aller Winkel der Hemisphäre über der Oberfläche
### Raumwinkel
- Dreidimensionales Gegenstück zum 2D-Winkel
- Raumwinkel $\Omega$ einer Fläche $A$ entspricht **Quotienten** der Fläche $S$, wenn $A$ auf eine Kugel vom Radius $r$ projiziert wird
- $\Omega = {S \over r^2}$
- Bei konstanter Größe nimmt der Raumwinkel einer Fläche quadratisch mit dem Abstand vom Zentrum ab
- Einheit **Steradiant** (sr)
### Strahlungsfluss
- Strahlungsfluss $\Phi$ = **Strahlungsenergie pro Zeit**
- Summe der Photonen-Energien, die pro Zeitraum $\Delta t$ emittiert werden
- Einheit: **Watt**
### Strahlstärke
- Strahlstärke $I$= **Strahlungsfluss pro Raumwinkel**
- Summe der Photonen-Energien die pro **Zeit und Raumwinkel** emittiert werden
- Wird benötigt, wenn Lichtquelle beispielsweise nicht in alle Richtungen gleich stark abstrahlt
- Einheit: **Watt pro Steradiant**
### Bestrahlungsstärke
- Bestrahlungsstärke $E$ = **Strahlungsfluss pro Flächenelement**
- einfallende Photonen-Energie **pro Zeit pro Flächenelement**
- Strahlungsfluss kommt aus allen Richtungen der Hemisphäre über der Fläche
- Einheit **Watt pro Quadratmeter**
### Strahldichte
- Strahldichte $L$ = **Strahlungsfluss pro Raumwinkel und sichtbarer Fläche**
- Strahlungsfluss in Richtung Auge
- Entspricht beobachteter Helligkeit
- Einheit: **Watt pro Steradiant pro Quadratmeter**
### BRDF (Bidirectional Reflection Distribution Function)
- Beschreibt den **winkelabhängigen spektralen Reflexionsfaktor einer Oberfläche** durch das Verhältnis von **reflektierter Strahldichte $L_o$** zur **einfallenden Bestrahlungsstärke $E$**
- $f_r(v,l)$
- $v \rightarrow$ ausgehende Richtung
- $l \rightarrow$ eingehende Richtung
- $v$ und $l$ können mit Winkeln parametrisiert werden
- 4-dimensionale Funktion, welche die **Reflexionseigenschaften einer Fläche** sehr genau beschreiben
- Reflexionseigenschaften sind in Materialdatenbanken (4D-Tabellen) abgelegt
- Da 4D-Tabellen viel Speicher benötigen und Materialien sich nicht direkt editieren lassen $\rightarrow$ Verwendung von parametrischen BRDF-Modellen (Phong, Blinn-Phong, Cook-Torrance, etc)
#### BRDF Eigenschaften
- Immer positiv
- **Helmholtz Reziprozität $\rightarrow$** eingehende und ausgehende Richtung können vertauscht werden
- Energieerhaltung ist $\leq 1$
## Path Tracing
- Ziel: **Effizientes, optisch korrektes Approximieren der Rendering Gleichung**
- Ansatz: Weiterverfolgung **nur eines zufälligen Strahls**
- nicht alle Punkte gleichermaßen berechnen, sondern priorisiert die, die den größten optischen Einfluss haben $\rightarrow$ *abhängig von passender WDF*
- Erste Möglichkeit: Approximation mittels Riemann-Summe
- Integral wird in Summenformel umgewandelt
- immernoch **ineffizient, da gleichförmige Abtastung**
### Importance Sampling
- Durch **Importance Sampling Theorie** kann jedes Integral auch durch eine Summe approximiert werden
- benutzt beliebige **Wahrscheinlichkeitsdichtefunktion** (WDF), welche die Bedingung $\int_a^b p(x) dx = 1$ erfüllen muss
- beste WDF wäre, wenn diese der Form der Funktion folgt
- $p(x)=\int_a^b{f(x)}$
- Dichte sollte höher sein, wenn Funktionswerte höher sind
- **verhindert Spikes**
- **Inversionsmethode**
- Ziel: Möglichst gutes Ergebnis nach wenig Abtastwerten $\rightarrow$ WDF so wählen, dass sie Form der Funktion folgt
- Ermöglicht die Erzeugung von **Zufallszahlen nach WDF (nicht linear) aus gleichverteilten Zufallszahlen**
### Auswerten der Rendering-Gleichung
- Problem bisherigen Ansatzes
- rekursive Strahlverfolgung **bei diffuser BRDF und kleiner Lichtquelle** ineffizient/qualitativ schlecht
- Beitrag nur dann, wenn Strahl Lichtquelle trifft
## Rendering Gleichung
- berechnet die reflektierte Strahldichte $L_o (v)$ im Oberflächenpunkt $x$ mit Normalen $n$ in Richtung $v$
- wie strahlt das Licht an einem bestimmten Punkt in eine bestimmte Richtung zurück
- $ausgehende\ Strahldichte = selbst\ emittiert + \int{BRDF,\ eingehende\ Strahldichte}$
- $L_O(v) = L_e(v) + \int_{\Omega}f_r(v,l)\ \underbrace{L_i(l)\ cos(\Theta)d\omega}_{dE(l)}$
- $L_O(v) \rightarrow$ ausgehende Strahldichte
- $L_e(v) \rightarrow$ von Fläche selbst emittierte Strahldichte
- $L_i(l) \rightarrow$ eingehende Strahldichte
- $E(l) \rightarrow$ Bestrahlungsstärke
- $f_r(v,l) \rightarrow$ BRDF
- $\Omega \rightarrow$ Gesamtheit aller Winkel der Hemisphäre über der Oberfläche
### Raumwinkel
- Dreidimensionales Gegenstück zum 2D-Winkel
- Raumwinkel $\Omega$ einer Fläche $A$ entspricht **Quotienten** der Fläche $S$, wenn $A$ auf eine Kugel vom Radius $r$ projiziert wird
- $\Omega = {S \over r^2}$
- Bei konstanter Größe nimmt der Raumwinkel einer Fläche quadratisch mit dem Abstand vom Zentrum ab
- Einheit **Steradiant** (sr)
### Strahlungsfluss
- Strahlungsfluss $\Phi$ = **Strahlungsenergie pro Zeit**
- Summe der Photonen-Energien, die pro Zeitraum $\Delta t$ emittiert werden
- Einheit: **Watt**
### Strahlstärke
- Strahlstärke $I$= **Strahlungsfluss pro Raumwinkel**
- Summe der Photonen-Energien die pro **Zeit und Raumwinkel** emittiert werden
- Wird benötigt, wenn Lichtquelle beispielsweise nicht in alle Richtungen gleich stark abstrahlt
- Einheit: **Watt pro Steradiant**
### Bestrahlungsstärke
- Bestrahlungsstärke $E$ = **Strahlungsfluss pro Flächenelement**
- einfallende Photonen-Energie **pro Zeit pro Flächenelement**
- Strahlungsfluss kommt aus allen Richtungen der Hemisphäre über der Fläche
- Einheit **Watt pro Quadratmeter**
### Strahldichte
- Strahldichte $L$ = **Strahlungsfluss pro Raumwinkel und sichtbarer Fläche**
- Strahlungsfluss in Richtung Auge
- Entspricht beobachteter Helligkeit
- Einheit: **Watt pro Steradiant pro Quadratmeter**
### BRDF (Bidirectional Reflection Distribution Function)
- Beschreibt den **winkelabhängigen spektralen Reflexionsfaktor einer Oberfläche** durch das Verhältnis von **reflektierter Strahldichte $L_o$** zur **einfallenden Bestrahlungsstärke $E$**
- $f_r(v,l)$
- $v \rightarrow$ ausgehende Richtung
- $l \rightarrow$ eingehende Richtung
- $v$ und $l$ können mit Winkeln parametrisiert werden
- 4-dimensionale Funktion, welche die **Reflexionseigenschaften einer Fläche** sehr genau beschreiben
- Reflexionseigenschaften sind in Materialdatenbanken (4D-Tabellen) abgelegt
- Da 4D-Tabellen viel Speicher benötigen und Materialien sich nicht direkt editieren lassen $\rightarrow$ Verwendung von parametrischen BRDF-Modellen (Phong, Blinn-Phong, Cook-Torrance, etc)
#### BRDF Eigenschaften
- Immer positiv
- **Helmholtz Reziprozität $\rightarrow$** eingehende und ausgehende Richtung können vertauscht werden
- Energieerhaltung ist $\leq 1$
## Path Tracing
- Ziel: **Effizientes, optisch korrektes Approximieren der Rendering Gleichung**
- Ansatz: Weiterverfolgung **nur eines zufälligen Strahls**
- nicht alle Punkte gleichermaßen berechnen, sondern priorisiert die, die den größten optischen Einfluss haben $\rightarrow$ *abhängig von passender WDF*
- Erste Möglichkeit: Approximation mittels Riemann-Summe
- Integral wird in Summenformel umgewandelt
- immernoch **ineffizient, da gleichförmige Abtastung**
### Importance Sampling
- Durch **Importance Sampling Theorie** kann jedes Integral auch durch eine Summe approximiert werden
- benutzt beliebige **Wahrscheinlichkeitsdichtefunktion** (WDF), welche die Bedingung $\int_a^b p(x) dx = 1$ erfüllen muss
- beste WDF wäre, wenn diese der Form der Funktion folgt
- $p(x)=\int_a^b{f(x)}$
- Dichte sollte höher sein, wenn Funktionswerte höher sind
- **verhindert Spikes**
- **Inversionsmethode**
- Ziel: Möglichst gutes Ergebnis nach wenig Abtastwerten $\rightarrow$ WDF so wählen, dass sie Form der Funktion folgt
- Ermöglicht die Erzeugung von **Zufallszahlen nach WDF (nicht linear) aus gleichverteilten Zufallszahlen**
### Auswerten der Rendering-Gleichung
- Problem bisherigen Ansatzes
- rekursive Strahlverfolgung **bei diffuser BRDF und kleiner Lichtquelle** ineffizient/qualitativ schlecht
- Beitrag nur dann, wenn Strahl Lichtquelle trifft
 - **Lösung**: Aufteilen der Rendering-Gleichung in **direkten und indirekten Anteil**
- direkter Anteil: **direkter Beitrag der Lichtquelle** *(Überprüfung mittels Schattenstrahl)*
- nicht mehr über kompletten Halbraum integrieren, sondern **nur über Raumwinkel der Lichtquelle**
- indirekter Anteil: Weiterverfolgen **zufälliger Richtung im Halbraum**
- Beitrag von direkter Lichtquelle hier verwerfen, um ihn nicht doppelt zu zählen
## PBR (physically-based Rendering) Materialen
- Materialen werden beschrieben durch eine Kombination von **transmittivem, reflektivem und streuendem** *(scattering)* Anteil
- Koponenten der **BSRF**:
- BRDF Dielektrika *(R = reflection)*
- BRDF Metalle
- BTDF *(T = transmission)*
- Emission
- Klarlack (clear coat)
- Glanz (sheen)
- Subsurface scattering
### Micofacetten BRDF
- Oberfläche wird aus Microfacetten beschrieben
- **Lösung**: Aufteilen der Rendering-Gleichung in **direkten und indirekten Anteil**
- direkter Anteil: **direkter Beitrag der Lichtquelle** *(Überprüfung mittels Schattenstrahl)*
- nicht mehr über kompletten Halbraum integrieren, sondern **nur über Raumwinkel der Lichtquelle**
- indirekter Anteil: Weiterverfolgen **zufälliger Richtung im Halbraum**
- Beitrag von direkter Lichtquelle hier verwerfen, um ihn nicht doppelt zu zählen
## PBR (physically-based Rendering) Materialen
- Materialen werden beschrieben durch eine Kombination von **transmittivem, reflektivem und streuendem** *(scattering)* Anteil
- Koponenten der **BSRF**:
- BRDF Dielektrika *(R = reflection)*
- BRDF Metalle
- BTDF *(T = transmission)*
- Emission
- Klarlack (clear coat)
- Glanz (sheen)
- Subsurface scattering
### Micofacetten BRDF
- Oberfläche wird aus Microfacetten beschrieben
 - zusammengesetzt aus **diffusem** *(konsant)*
- und **spekularem** Anteil
- **Fresnel**-Reflexionsgrad
- Verteilung der Microfacetten ***(Rauheit)***
- Geometriefaktor ***(Selbstbeschattung)***
- zusammengesetzt aus **diffusem** *(konsant)*
- und **spekularem** Anteil
- **Fresnel**-Reflexionsgrad
- Verteilung der Microfacetten ***(Rauheit)***
- Geometriefaktor ***(Selbstbeschattung)***
 ### Fresnel Reflexion
- reflexiver und transmittiever Anteil hängen von Einfallswinkel und Brechungsindex des Materials ab
- **Refraktion:** Brechung an Oberfläche
- optisch dünner $\rightarrow$ optisch dichter: Brechung zur Normalen hin
- optisch dichter $\rightarrow$ optisch dünner: Brechung von Normalen weg
- **Berechungsmöglichkeiten:** **Cook Torrance** oder **Schlick** *(Approximation, schneller)*
#### Fresnel Reflexion: Dielektrika
- winkelabhängig wird entweder reflektiert, transmittiert oder absorbiert
- **reflektiver Anteil** wird an Microfacetten gestreut $\rightarrow$ **spekularer Anteil** der Reflexion
- **transmittiver Anteil** wird bei opaken *(durchsichtigen)* unter der Oberfläche zufällig abgelenkt *(tlws. absorbiert)* $\rightarrow$ **diffuser Anteil** der Reflexion
- mehr Licht reflektiert $\rightarrow$ weniger Licht transmittiert $\rightarrow$ geringerer diffuser Anteil
- reflexiver und transmittiever Anteil hängen von Einfallswinkel und Brechungsindex des Materials ab
### Fresnel Reflexion
- reflexiver und transmittiever Anteil hängen von Einfallswinkel und Brechungsindex des Materials ab
- **Refraktion:** Brechung an Oberfläche
- optisch dünner $\rightarrow$ optisch dichter: Brechung zur Normalen hin
- optisch dichter $\rightarrow$ optisch dünner: Brechung von Normalen weg
- **Berechungsmöglichkeiten:** **Cook Torrance** oder **Schlick** *(Approximation, schneller)*
#### Fresnel Reflexion: Dielektrika
- winkelabhängig wird entweder reflektiert, transmittiert oder absorbiert
- **reflektiver Anteil** wird an Microfacetten gestreut $\rightarrow$ **spekularer Anteil** der Reflexion
- **transmittiver Anteil** wird bei opaken *(durchsichtigen)* unter der Oberfläche zufällig abgelenkt *(tlws. absorbiert)* $\rightarrow$ **diffuser Anteil** der Reflexion
- mehr Licht reflektiert $\rightarrow$ weniger Licht transmittiert $\rightarrow$ geringerer diffuser Anteil
- reflexiver und transmittiever Anteil hängen von Einfallswinkel und Brechungsindex des Materials ab
 #### Fresnel Reflexion: Metalle
- transmittiver Anteil wird absorbiert $\rightarrow$ **keine diffuse Reflexion**
- **spekularer Anteil** ist **farbig**, da reflektierter Anteil abhängig von Wellenlänge
#### Fresnel Reflexion: Metalle
- transmittiver Anteil wird absorbiert $\rightarrow$ **keine diffuse Reflexion**
- **spekularer Anteil** ist **farbig**, da reflektierter Anteil abhängig von Wellenlänge
 ## Bildbasierte Beleuchtung
- **emmitierte Strahldichte** $L_i$ der Umgebung wird **durch sphärisches Umgebungsbild** *(Environment Map)* angegeben
- Zusammenhang zwischen Textur- und Kugelkoordinaten
### Importance Sampling der Environment Map
- Umbegungsbild wird in **Grauwertbild** $g(s,t)$ umgewandelt
- Parametrisierung in Texturkoordinaten: $s, t \in [0,1]$
- Verteilungsfunktion kann nicht invertiert werden, da nicht nach Zufallsvariable aufgelöst werden kann, daher:
- **zeilenweises** Durchlaufen, bis Zufallsvariable erreicht $\rightarrow$ Zeile, in der Abtastwert genommen wird
- **spaltenweises** Durchlaufen, bis Zufallsvariable erreicht $\rightarrow$ Abtastpunkt
## Multiple Importance Sampling
- **Problem:** Da **BRDF** druch **WDF** geteilt wird, entstehen extrem hohe Sample-Werte, wo **WDF** sehr gering $\rightarrow$ Noise
- also wenn **BRDF** bzw. $f$ **groß** und **WDF** bzw. $p$ **klein**
- grobes Prinzip: Nutzung bisherigen Durchschnitts und Erwartungswerten zur Entscheidung der Sampling-Methode
- **Ziel:** Verminderung von Noise durch Kombination verschiedener Sampling-Verfahren
- nur **BRDF**-Sampling:
- gut auf stark reflektiven Materialien
- schlecht bei matteren Materialien
- nur **Light**-Sampling
- gut auf matteren Materialien
- schlecht auf stark reflektiven Materialien
## Bildbasierte Beleuchtung
- **emmitierte Strahldichte** $L_i$ der Umgebung wird **durch sphärisches Umgebungsbild** *(Environment Map)* angegeben
- Zusammenhang zwischen Textur- und Kugelkoordinaten
### Importance Sampling der Environment Map
- Umbegungsbild wird in **Grauwertbild** $g(s,t)$ umgewandelt
- Parametrisierung in Texturkoordinaten: $s, t \in [0,1]$
- Verteilungsfunktion kann nicht invertiert werden, da nicht nach Zufallsvariable aufgelöst werden kann, daher:
- **zeilenweises** Durchlaufen, bis Zufallsvariable erreicht $\rightarrow$ Zeile, in der Abtastwert genommen wird
- **spaltenweises** Durchlaufen, bis Zufallsvariable erreicht $\rightarrow$ Abtastpunkt
## Multiple Importance Sampling
- **Problem:** Da **BRDF** druch **WDF** geteilt wird, entstehen extrem hohe Sample-Werte, wo **WDF** sehr gering $\rightarrow$ Noise
- also wenn **BRDF** bzw. $f$ **groß** und **WDF** bzw. $p$ **klein**
- grobes Prinzip: Nutzung bisherigen Durchschnitts und Erwartungswerten zur Entscheidung der Sampling-Methode
- **Ziel:** Verminderung von Noise durch Kombination verschiedener Sampling-Verfahren
- nur **BRDF**-Sampling:
- gut auf stark reflektiven Materialien
- schlecht bei matteren Materialien
- nur **Light**-Sampling
- gut auf matteren Materialien
- schlecht auf stark reflektiven Materialien